Пример создания рекуррентной нейронной сети в Python (Часть 1)

Сегодня мы поговорим о том, что подразумевается под рекуррентными нейронными сетями, в чем их особенности что делать для их создания с нуля.

Что такое нейронная сеть?

Сперва давайте поймем, что такое нейронные сети вообще. Это специальная математическая модель, которая работает по такому же принципу, как человеческий мозг. В основе нейронной сети лежат искусственные нейроны – специальные вычислительные элементы, которые создавались на основе нейронов в живых организмах.

Нейросети применяются в широком спектре областей жизни. Они умеют распознавать лица (в том числе, определять преступников), выполнять диагностику заболеваний (в будущем, говорят, они это будут делать лучше, чем люди).  Голосовые помощники в смартфонах и маски в развлекательных приложениях – это также примеры работы нейросетей.

Конечно, искусственная нейронная сеть все же отличается от человеческого мозга. Чтобы искусственные нейроны работали, требуются колоссальные вычислительные мощности. Да и связей между нейронами в человеческом мозгу значительно больше, чем даже в самой сложной нейросети. 

Помимо всего прочего, человеческий мозг отличается от компьютера еще и тем, что он может выполнять множество процессов одновременно. Компьютер же любую задачу, даже простую, будет разбивать на последовательность действий.

Главное достоинство любых нейронных сетей в том, что они требуют минимальной работы с признаками. Нейронные сети можно обучать на сырых данных.

Спектр задач, которые могут решаться нейросетями, с каждым годом становится все более широким:

1. Поиск людей по фотографии, в том числе, по картине.
2. Игра в шахматы с программой, которая пишет текст, а не играет в шахматы.
3. Создание приложений для изменения лиц на видео.
4. Массовое распространение фейков.
5. Раскрашивание черно-белых снимков.

И множество других задач. Одним словом, работа с нейросетями – очень интересная составляющая программирования. Поэтому давайте теперь приступим к рассмотрению отдельной разновидности нейросетей.

Рекуррентные нейронные сети – зачем используются?

Что такое рекуррентные нейронные сети? Это разновидность нейросетей, которая используется для обработки последовательностей. В частности, они полезны для анализа текста. 

Один из главных аспектов, характеризующих работу с нейросетями, в том, что они используют параметры, которые предварительно заданы и которые используются в машинном обучении.

Главное преимущество рекуррентных нейросетей заключается в том, что они обрабатывают последовательности с изменчивыми длинами как для ввода, так и для выхода. 

Рекуррентные сети выглядят по-разному. Приведем некоторые примеры того, какими они бывают.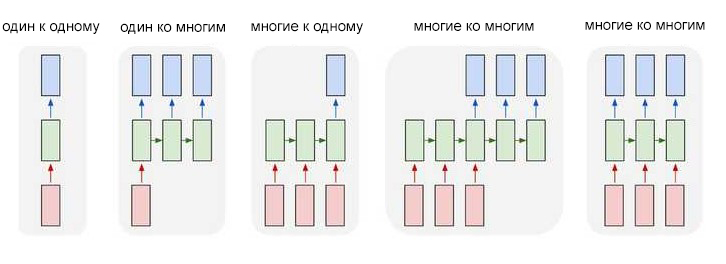

Почему такие нейросети полезны? Потому что они умеют обрабатывать последовательности. Это делает возможным их использование в целом комплексе сфер:

1. Машинный перевод. Все знают Google Translate. Так вот, этот онлайн-переводчик использует рекуррентные нейросети. Сначала в них передается текст, который потом выводит обработанный вариант. 
2. Анализ настроений. Точно так же, как и в предыдущем варианте, для этого используются рекуррентные сети с принципом «один к одному». Например, с их помощью можно понять, пользователь оставил позитивный отклик или негативный. 

Далее мы рассмотрим то, как правильно использовать рекуррентные нейросети для анализа настроений.

Пример создания рекуррентной нейросети

Допустим, что мы имеем нейросеть, работающую по описанному ранее принципу. Входящие данные – x0, х1, … xn, а результаты вывода — y0, y1, … yn. Данные xi и yi – это векторы и бывают любых размеров.

Далее мы вместо длинного названия «рекуррентные нейронные сети» будем использовать аббревиатуру RNN. Так вот, они работают по принципу итерированного обновления скрытого состояния h. Этот вектор может иметь разный размер. Тем не менее, нужно учитывать следующее:

1. Следующее скрытое состояние ht определяется с помощью предыдущего ht-1, а также дальнейшего ввода xt.
2. Дальнейший вывод yt определяется с помощью ht.

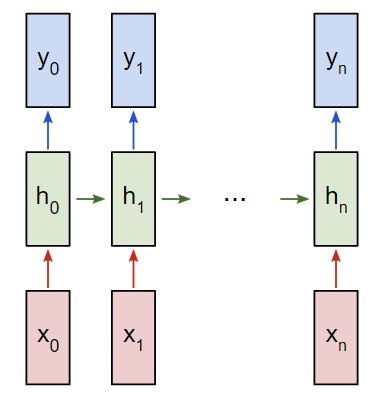
Именно это и делает нейросеть рекуррентной. На каждом этапе она использует одинаковый весовой коэффициент. Проще говоря, классическая RNN задействует лишь три набора параметров веса для выполнения подсчетов.

• Wxh применяется для связок xt → ht

• Whh применяется для связок ht-1 → ht
• Why применяется для связок ht → yt

Также используется два смещения для рекуррентной нейросети:

• bh добавляется при подсчете ht
• by добавляется при подсчете yt

Вес здесь – это матрица, а смещение – вектор. Здесь RNN имеет три параметра и два смещения. 

Все описанное выше может быть выражено в таких уравнениях: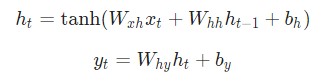

Внимательно изучите этот пример. Вообще, разбор уравнений в этой инструкции пропускать не рекомендуется. Не забывайте, что вес – это матрица, а другие переменные – вектора.

Когда речь идет о весе, выполняется матричное умножение. После его выполнения векторы записываются в итоговый результат. После этого используется гиперболическая функция. Она играет роль функции активации для первого уравнения. Также возможно применение и других методов активации, например, сигмоиды. 

Задача функции активации – подключать несвязанные входные данные с выводом, у которого простая и предсказуемая форма. Обычно в качестве нее используется сигмоида.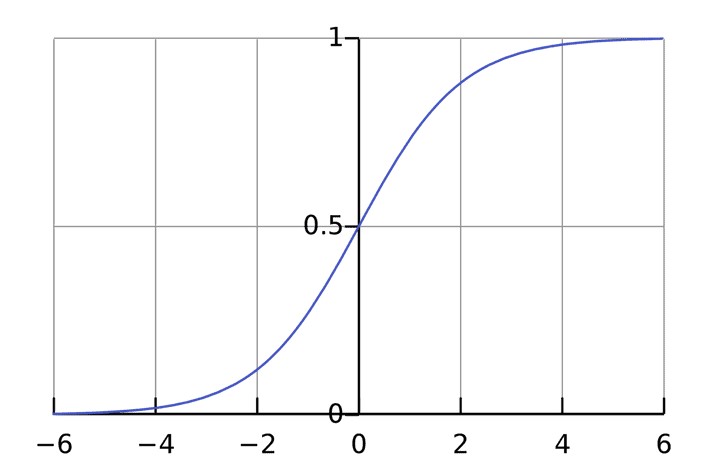

Постановка задачи

Давайте попробуем создать RNN, которая выполняет анализ настроения. Далее мы дадим задачу определить модальность строки, которая передается на вход. Вот некоторые примеры данных, которые будут интерпретироваться RNN.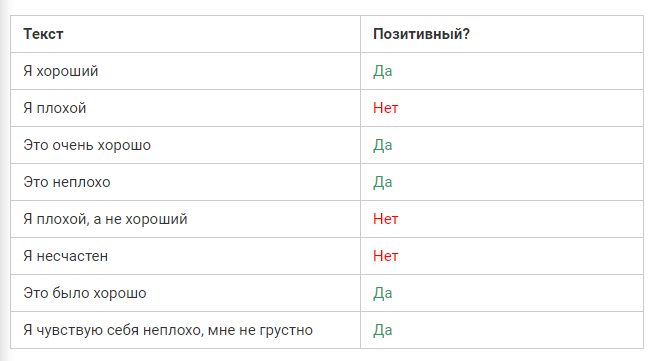

Составление плана

Здесь будем приводить рекуррентную сеть типа «многие к одному». В целом, ее принцип аналогичен схеме «многие к многим». Тем не менее, для одного пункта вывода y будет использоваться лишь скрытое состояние.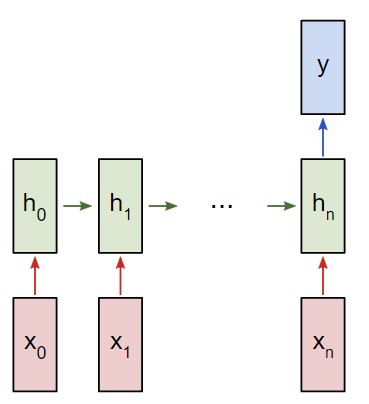

Каждый xi будет вектором, который представляет конкретное слово. В свою очередь вектор y будет выводом, в котором будет два числовых значения. Одно являет собой позитивное настроение, а другое – отрицательное. Для превращения этих значений в вероятности будет применяться функция Softmax. 

Что это за функция? Это обобщение логистической функции для многомерного случая. Она представлена следующей формулой.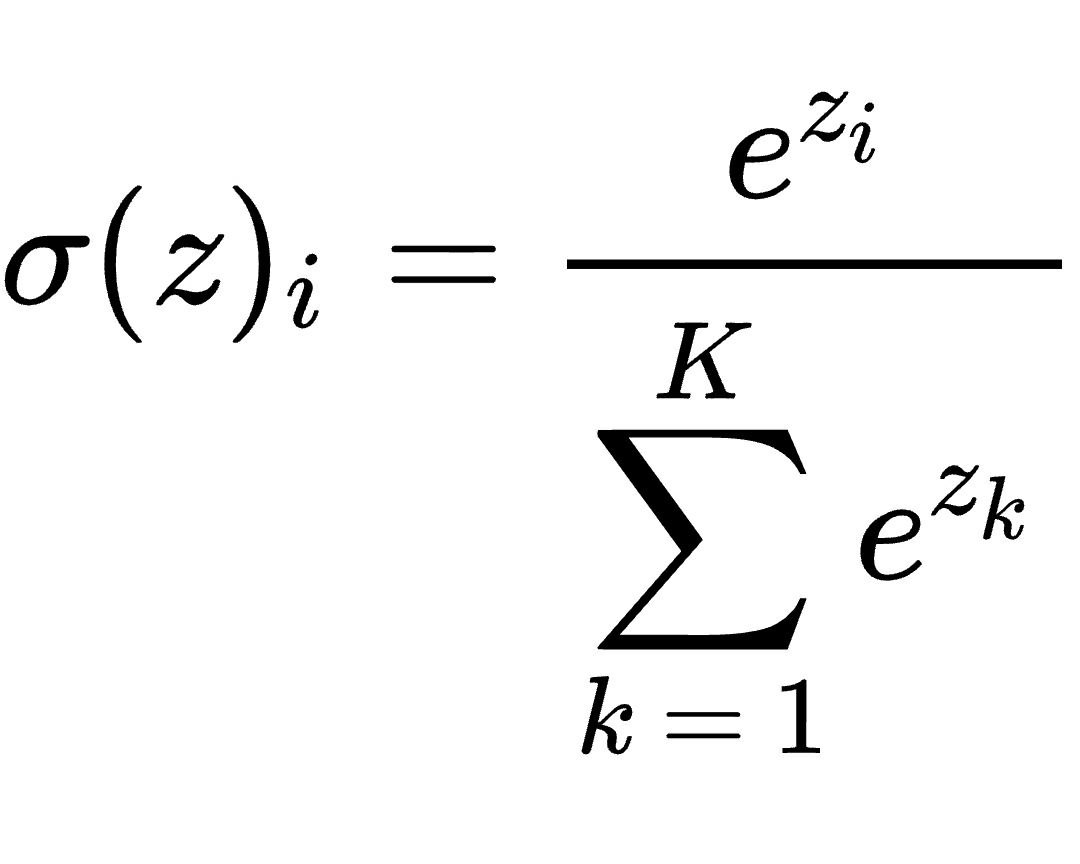

А теперь давайте начнем создавать рекуррентную нейросеть.

Предварительная обработка

Набор данных, который приводился ранее, включает два Python-словаря.  

train_data = {

    'good': True,

    'bad': False,

    # ... больше данных

}

 

test_data = {

    'this is happy': True,

    'i am good': True,

    # ... больше данных

}

True = Позитивное, False = Ложное

Чтобы получить данные в удобном формате, нужно будет сделать предварительную проверку. Сперва надо создать словарь из всех слов, которые указываются в наборе данных. 

from data import train_data, test_data




# Создание словаря

vocab = list(set([w for text in train_data.keys() for w in text.split(' ')]))

vocab_size = len(vocab)




print('%d unique words found' % vocab_size) # найдено 18 уникальных слов

vocab с этого момента включает список всех слов, употребляемых по крайней мере в одном тексте. Теперь каждому из слов присвоим индекс целочисленного типа. 

# Назначить индекс каждому слову

word_to_idx = { w: i for i, w in enumerate(vocab) }

idx_to_word = { i: w for i, w in enumerate(vocab) }

 

print(word_to_idx['good']) # 16 (это может измениться)

print(idx_to_word[0]) # грустно (это может измениться)

Теперь можно применять индекс целого числа для отображения любого заданного слова. Почему это важно? Дело в том, что рекуррентная нейросеть может различать исключительно числа. Поэтому любое слово должно быть предварительно конвертировано в число определенной модальности. 

Важно напомнить, что каждый ввод xi – это вектор. Нами будут использоваться векторы, представленные в форме унитарного кода. В каждом векторе единица будет расположена в соответствующем индексе целочисленного типа. 

Поскольку в словаре 18 уникальных слов, каждый xi будет 18-мерным унитарным вектором. 

import numpy as np

 

 

def createInputs(text):

    '''

    Возвращает массив унитарных векторов

    которые представляют слова в введенной строке текста

    - текст является строкой string

    - унитарный вектор имеет форму (vocab_size, 1)

    '''

    

    inputs = []

    for w in text.split(' '):

        v = np.zeros((vocab_size, 1))

        v[word_to_idx[w]] = 1

        inputs.append(v)

    

    return inputs

Позже мы будем использовать createInputs() для генерации входящих данных в виде векторов. А потом передадим их в рекуррентную нейронную сеть. 

Прямое распространение нейросети

Итак, давайте теперь непосредственно создадим нашу нейросеть. Для начала необходимо выполнить инициализацию, используя три параметра веса и два смещения. 

import numpy as np

from numpy.random import randn

 

 

class RNN:

    # Классическая рекуррентная нейронная сеть

    

    def __init__(self, input_size, output_size, hidden_size=64):

        # Вес

        self.Whh = randn(hidden_size, hidden_size) / 1000

        self.Wxh = randn(hidden_size, input_size) / 1000

        self.Why = randn(output_size, hidden_size) / 1000

        

        # Смещения

        self.bh = np.zeros((hidden_size, 1))

        self.by = np.zeros((output_size, 1))

Учтите то, что для устранения внутренней вариативности весов в этом примере выполняется операция деления на 1000. Но это далеко не самый лучший вариант действий. Но поскольку так проще всего поступать, то данный пример становится более понятным для начинающих разработчиков.

С помощью функции np.random.randn() выполняется инициализация веса из нормального распределения. Ну и после этого будет реализована прямая передача рассматриваемой нейросети. 

Вспомните те два уравнения, которые давались в начале этой статьи.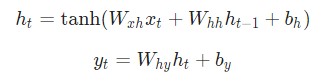

Если реализовать эти уравнения в коде, результат получится следующим. 

class RNN:

    # ...

    

    def forward(self, inputs):

        '''

        Выполнение передачи нейронной сети при помощи входных данных

        Возвращение результатов вывода и скрытого состояния

        Вывод - это массив одного унитарного вектора с формой (input_size, 1)

        '''

        h = np.zeros((self.Whh.shape[0], 1))

        

        # Выполнение каждого шага в нейронной сети RNN

        for i, x in enumerate(inputs):

            h = np.tanh(self.Wxh @ x + self.Whh @ h + self.bh)

        

        # Compute the output

        y = self.Why @ h + self.by

        

        return y, h

Согласитесь, что это достаточно легко. Учтите то, что была инициализация h для нулевого вектора на первом этапе, поскольку не было предыдущего h, который можно было бы применить.

Теперь попробуем сделать так: 

...

def softmax(xs):

    # Применение функции Softmax для входного массива

    return np.exp(xs) / sum(np.exp(xs))

 

 

# Инициализация нашей рекуррентной нейронной сети RNN

rnn = RNN(vocab_size, 2)

 

 

inputs = createInputs('i am very good')

out, h = rnn.forward(inputs)

probs = softmax(out)

print(probs) # [[0.50000095], [0.49999905]]

Конечно, рекуррентная сеть, созданная в этом примере, работает. Тем не менее, она точно не имеет нужной нам функциональности. Исправим эту проблему.

Обратное распространение нейросети

Нам надо тренировать нейросеть. Для этого надо использовать функцию потери. В этом примере будет задействоваться потеря перекрестной энтропии, которая в подавляющем числе ситуаций совместима с Softmax. Для подсчета будет использоваться следующая формула.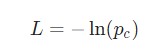

В этом случае под pc подразумевается предсказуемая вероятность рекуррентной нейронной сети для класса correct (положительный или отрицательный). Так, если текст положительной модальности предсказывается сетью, как положительный на 90%, то потеря рассчитывается таким образом.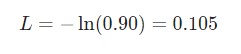

Если есть параметры, нейронная сеть может быть натренирована так, чтобы использовался градиентный спуск для уменьшения потерь. Соответственно, тут нам нужны будут градиенты.

Выводы

Таким образом, мы разобрались в основах использования рекуррентных нейронных сетей. Но, конечно же, это не все, что вам требуется знать. Дальше мы рассмотрим этот вопрос более глубоко. 

Перед тем, как изучать следующую часть, необходимо разобраться, что такое многовариантное исчисление и как оно устроено. Только тогда примеры в следующей статье будут понятными.