В прошлой части этого руководства мы рассмотрели, что такое нейронные сети, для чего они используются. Также мы поняли, в чем особенность рекуррентных нейросетей и то, как они работают. Теперь мы будем создавать такую сеть в Python. Не забывайте о том, что необходимо иметь базовые представления о том, что такое многовариантное исчисление, чтобы понимать, как работать материалом этого руководства.
Параметры нейронной сети
В дальнейшем будут задействоваться такие параметры.
- y — информация на входе нейросети;
- р — итоговая вероятность: р = softmax(y);
- с — истинная метка конкретного образца текста, так названный «правильный» класс;
- L — потеря перекрестной энтропии: L = -ln(pc);
- Wxh, Whh и Why — три весовые матрицы в нейронной сети;
- bh и by — два вектора смещения в рассматриваемой рекуррентной сети RNN.
Установка
Теперь необходимо задать конфигурацию фазы прямого распространения. Это требуется, чтобы кешировать отдельные данные, применяемые в фазе обратного распространения нейросети.
Одновременно с этим, будет возможна установка основного скелета для этапа обратного распространения. Код, отвечающий за реализацию этого, будет иметь следующий вид.
class RNN:
# ...
def forward(self, inputs):
'''
Выполнение фазы прямого распространения нейронной сети с
использованием введенных данных.
Возврат итоговой выдачи и скрытого состояния.
- Входные данные в массиве однозначного вектора с формой (input_size, 1).
'''
h = np.zeros((self.Whh.shape[0], 1))
self.last_inputs = inputs
self.last_hs = { 0: h }
# Выполнение каждого шага нейронной сети RNN
for i, x in enumerate(inputs):
h = np.tanh(self.Wxh @ x + self.Whh @ h + self.bh)
self.last_hs[i + 1] = h
# Подсчет вывода
y = self.Why @ h + self.by
return y, h
def backprop(self, d_y, learn_rate=2e-2):
'''
Выполнение фазы обратного распространения нейронной сети RNN.
- d_y (dL/dy) имеет форму (output_size, 1).
- learn_rate является вещественным числом float.
'''
pass
Градиенты
А теперь наступило время математики. Для начала нужно вычислит.
Нам известны следующие данные.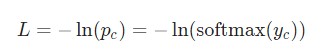
Здесь задействуется фактическое значениеа также происходит дифференцирование сложной функции. Мы получим такой результат.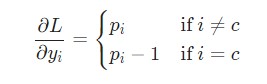
Например, если p = [0.2, 0.2, 0.6], а корректным классом является c=0, то тогда значение
будет равняться [-0.8, 0.2, 0.6]. И это выражение уже можно перевести в код.
# Цикл для каждого примера тренировки for x, y in train_data.items(): inputs = createInputs(x) target = int(y) # Прямое распространение out, _ = rnn.forward(inputs) probs = softmax(out) # Создание dL/dy d_L_d_y = probs d_L_d_y[target] -= 1 # Обратное распространение rnn.backprop(d_L_d_y)
Превосходно. Теперь давайте разберемся с градиентами для Why и by, используемые исключительно для перехода конечного скрытого состояния в результат вывода нейросети. Наши данные такие.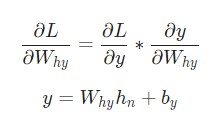
В этом случае hn – это конечное скрытое состояние. Следовательно,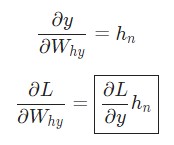 
Таким же образом выполняем расчет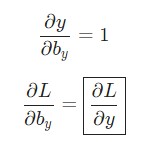
И, наконец, приступаем к реализации backprop().
class RNN: # ... def backprop(self, d_y, learn_rate=2e-2): ''' Выполнение фазы обратного распространения нейронной сети RNN. - d_y (dL/dy) имеет форму (output_size, 1). - learn_rate является вещественным числом float. ''' n = len(self.last_inputs) # Подсчет dL/dWhy и dL/dby. d_Why = d_y @ self.last_hs[n].T d_by = d_y
В предыдущих примерах уже были созданы self.last_hs в forward().
Итак, нам потребуются градиенты для Whh, Wxh и bh, которые применяются на каждом этапе нейросети. Мы имеем: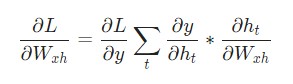
Изменение Wxh оказывает воздействие как на каждый ht, так и на все y. Это же вызывает изменения в L. Чтобы полностью определить градиент Wxh, нужно провести обратное распространение через каждый этап. Такой процесс также называется обратным распространением во времени либо BPTT (аббревиатура, которая означает перевод этого выражения на английский язык).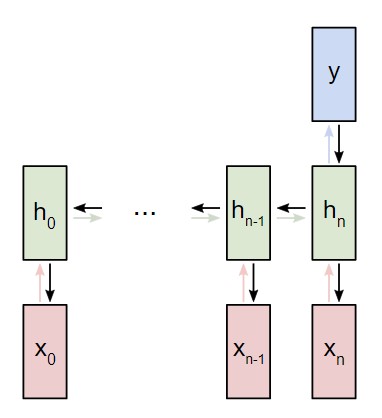
Wxh применяется для каждой прямой ссылки xt → ht. Следовательно, нам нужно провести обратное распространение назад к каждой из данных ссылок.
После того, как мы приблизились к определенному шагу t, необходимо определить
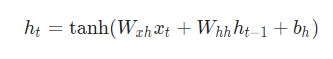
И мы уже владеем производной гиперболической функции tanh.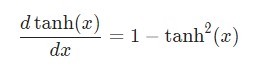
Теперь используем дифференцирование сложной функции, либо цепное правило.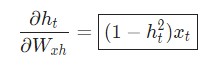
Производим расчеты точно таким же способом.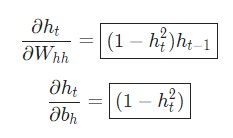
А далее выполняем такие расчеты.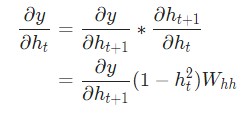
Теперь осуществляем реализацию обратного распространения во времени. Для этого нужно отталкиваться от скрытого состояния в роли первоначальной точки. Затем действия будут выполняться в противоположном порядке. Следовательно, на момент, когда осуществлялся подсчет dy/dht, мы уже будем знать, какое значение dy/dht+1. Единственное исключение здесь будет – это последнее скрытое состояние hn.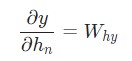
Теперь мы имеем все необходимое, чтобы закончить backprop() и реализовать BPTT.
class RNN:
# ...
def backprop(self, d_y, learn_rate=2e-2):
'''
Выполнение фазы обратного распространения RNN.
- d_y (dL/dy) имеет форму (output_size, 1).
- learn_rate является вещественным числом float.
'''
n = len(self.last_inputs)
# Вычисление dL/dWhy и dL/dby.
d_Why = d_y @ self.last_hs[n].T
d_by = d_y
# Инициализация dL/dWhh, dL/dWxh, и dL/dbh к нулю.
d_Whh = np.zeros(self.Whh.shape)
d_Wxh = np.zeros(self.Wxh.shape)
d_bh = np.zeros(self.bh.shape)
# Вычисление dL/dh для последнего h.
d_h = self.Why.T @ d_y
# Обратное распространение во времени.
for t in reversed(range(n)):
# Среднее значение: dL/dh * (1 - h^2)
temp = ((1 - self.last_hs[t + 1] ** 2) * d_h)
# dL/db = dL/dh * (1 - h^2)
d_bh += temp
# dL/dWhh = dL/dh * (1 - h^2) * h_{t-1}
d_Whh += temp @ self.last_hs[t].T
# dL/dWxh = dL/dh * (1 - h^2) * x
d_Wxh += temp @ self.last_inputs[t].T
# Далее dL/dh = dL/dh * (1 - h^2) * Whh
d_h = self.Whh @ temp
# Отсекаем, чтобы предотвратить разрыв градиентов.
for d in [d_Wxh, d_Whh, d_Why, d_bh, d_by]:
np.clip(d, -1, 1, out=d)
# Обновляем вес и смещение с использованием градиентного спуска.
self.Whh -= learn_rate * d_Whh
self.Wxh -= learn_rate * d_Wxh
self.Why -= learn_rate * d_Why
self.bh -= learn_rate * d_bh
self.by -= learn_rate * d_by
Следует учитывать такие аспекты:
- Для большего удобства
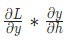были объединены. - Мы регулярно вносим изменения в переменную d_h, которая всегда актуальна. Она содержит значение dy/dht+1, которое используется для расчета dL/dht.
- После того, как с обратным распространением во времени будет покончено, необходимо использовать np.clip() на значениях градиента ниже -1 либо выше -1. Что это даст? Прежде всего, избавит от проблемы со взрывными градиентами. Такое происходит, когда градиенты чрезмерно увеличиваются в размерах из-за множества умноженных параметров. Взрыв, а также исчезновение градиентов происходят довольно часто. Для их обработки лучше использовать более сложные рекуррентные нейросети, например, LSTM.
- Когда подсчет всех градиентов будет завершен, необходимо будет обновить параметры веса и смещения путем применения градиентного спуска.
Итак, у нас получилось создать рекуррентную нейросеть. Отлично.
Тестирование рекуррентной сети
Итак, давайте теперь попробуем протестировать получившуюся нейросеть. Сперва необходимо написать вспомогательную функцию для обработки информации, которая передается этой нейронной сети.
import random def processData(data, backprop=True): ''' Возврат потери рекуррентной нейронной сети и точности для данных - данные представлены как словарь, что отображает текст как True или False. - backprop определяет, нужно ли использовать обратное распределение ''' items = list(data.items()) random.shuffle(items) loss = 0 num_correct = 0 for x, y in items: inputs = createInputs(x) target = int(y) # Прямое распределение out, _ = rnn.forward(inputs) probs = softmax(out) # Вычисление потери / точности loss -= np.log(probs[target]) num_correct += int(np.argmax(probs) == target) if backprop: # Создание dL/dy d_L_d_y = probs d_L_d_y[target] -= 1 # Обратное распределение rnn.backprop(d_L_d_y) return loss / len(data), num_correct / len(data)
И теперь, для тренировки возможно написание следующего цикла..
# Цикл тренировки
for epoch in range(1000):
train_loss, train_acc = processData(train_data)
if epoch % 100 == 99:
print('--- Epoch %d' % (epoch + 1))
print('Train:\tLoss %.3f | Accuracy: %.3f' % (train_loss, train_acc))
test_loss, test_acc = processData(test_data, backprop=False)
print('Test:\tLoss %.3f | Accuracy: %.3f' % (test_loss, test_acc))
После того, как запустить этот код, мы получим такой результат вывода.
--- Epoch 100 Train: Loss 0.688 | Accuracy: 0.517 Test: Loss 0.700 | Accuracy: 0.500 --- Epoch 200 Train: Loss 0.680 | Accuracy: 0.552 Test: Loss 0.717 | Accuracy: 0.450 --- Epoch 300 Train: Loss 0.593 | Accuracy: 0.655 Test: Loss 0.657 | Accuracy: 0.650 --- Epoch 400 Train: Loss 0.401 | Accuracy: 0.810 Test: Loss 0.689 | Accuracy: 0.650 --- Epoch 500 Train: Loss 0.312 | Accuracy: 0.862 Test: Loss 0.693 | Accuracy: 0.550 --- Epoch 600 Train: Loss 0.148 | Accuracy: 0.914 Test: Loss 0.404 | Accuracy: 0.800 --- Epoch 700 Train: Loss 0.008 | Accuracy: 1.000 Test: Loss 0.016 | Accuracy: 1.000 --- Epoch 800 Train: Loss 0.004 | Accuracy: 1.000 Test: Loss 0.007 | Accuracy: 1.000 --- Epoch 900 Train: Loss 0.002 | Accuracy: 1.000 Test: Loss 0.004 | Accuracy: 1.000 --- Epoch 1000 Train: Loss 0.002 | Accuracy: 1.000 Test: Loss 0.003 | Accuracy: 1.000
Довольно неплохо, не так ли? Особенно учитывая то, что эта нейросеть была спроектирована нами самостоятельно.
Выводы
Итак, на этом наше руководство по нейросетям подошло к концу. Мы теперь разбираемся в понятии RNN и принципе работы нейросетей этого типа. Также поняли, чем они полезны, как создавать и тренировать рекуррентные сети. Тем не менее, это – лишь капля в море. Если есть желание, вы всегда можете изучить эти темы самостоятельно. В этом вам могут помочь следующие ресурсы и темы:
- LTSM. С ней надо ознакомиться более подробно, поскольку это долгая краткосрочная память, которая позволяет более гибко настраивать RNN. Также рекомендуется почитать более подробно об управляемых рекуррентных блоках, которые являются популярной разновидностью LTSM.
- Экспериментируйте. Это главная составляющая обучающего процесса. В частности, нужно экспериментировать и с более сложными RNN. Например, можно использовать подходящие ML библиотеки, например, Tensofrflow, Keras либо PyTorch.
- Почитайте о двунаправленных нейросетях, обрабатывающих последовательности как в прямом, так и противоположном направлениях. Это дает возможность больше данных взять от вывода.
- Почитайте о векторном представлении слов. Для этого можно использовать GloVe либо Word2Vec.
- Почитайте также о Natural Language Toolkit (NLTK). Это популярная библиотека для Python, которая предназначена для работы с данными на языках, созданных для людей, а не компьютеров.
Одним словом, работа с нейронными сетями – это интересная, но сложная дисциплина. Она требует профессионального подхода и понимания, как устроено машинное обучение. К счастью, Python имеет достаточный инструментарий, чтобы настраивать нейронные сети. Это несколько сложнее, чем классическое программирование, где инструкции дает разработчик. Но это гораздо перспективнее. Будущее именно за этими приложениями. Успехов.
