В предыдущей части этого руководства мы рассмотрели особенности создания нейронных сетей. Сейчас продолжаем эту тему. Мы закончили в прошлый раз многовариантными исчислениями. У нас тогда накопилось большое количество формул, разобраться в которых новичку не так и просто. Чтобы сделать эту тему более понятной, давайте рассмотрим такой пример.
Расчет частных производных – пример
В этом примере мы будем использовать исключительно Alice.
Тут вес будет представлен в виде единицы, а смещение – нуля. Если выполним прямое распространение через сеть, получим такой результат.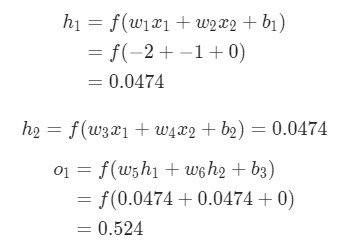
Результат вычислений, произведенных нейросетью, ypred = 0,524. Это дает нам небольшое понимание того, рассматривается мужчина или женщина. Давайте попробуем найти величину 
Напоминание: нами была выведена f ‘(x) = f (x) * (1 — f (x)) прежде для нашей сигмоиды.
Успех! Результат свидетельствует о том, что если мы пытаемся увеличить w1, L несколько увеличивается.
Использование стохастического градиентного спуска для тренировки нейронной сети
Мы владеем всем требуемым инструментарием, чтобы обучить нейросеть. Нами используется алгоритм оптимизации, который называется стохастическим градиентным спуском (SGD), который говорит нам, как правильно изменять вес и смещение, чтобы потери были минимальными. Фактически это выражается в таком уравнении.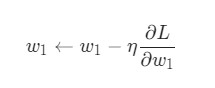
η – это константа, которая называется оценкой обучения. Она отвечает за то, чтобы контролировать скорость тренировки нейронной сети. Все, что нами делается, так это вычитание 
из w1.
- Если значение
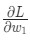положительное, то w1 уменьшится. Как следствие, L также станет меньше. - Если значение
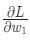отрицательное, то w1 станет больше.
Если это правило применить на каждый вес и смещение в сети, то потеря будет постепенно уменьшаться. В свою очередь, показатели сети станут лучше.
Наш процесс обучения будет выглядеть так:
- Выбираем один пункт из набора данных, который мы имеем. Это то, благодаря чему он и становится стохастическим градиентным спуском. Нами обрабатывается исключительно один пункт за одну итерацию.
- Рассчитываются все частные производные потери по весу либо смещению. Это могут быть разные числа:
, 
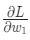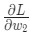и так далее. - Воспользовавшись уравнением обновления, обновим каждый вес и смещение.
- Возвращаемся к первому пункту.
А теперь давайте проанализируем, как это работает на практике.
Как создать нейросеть с нуля на Python
Итак, давайте теперь создадим готовую нейросеть. Она будет иметь следующие вводные данные и структуру.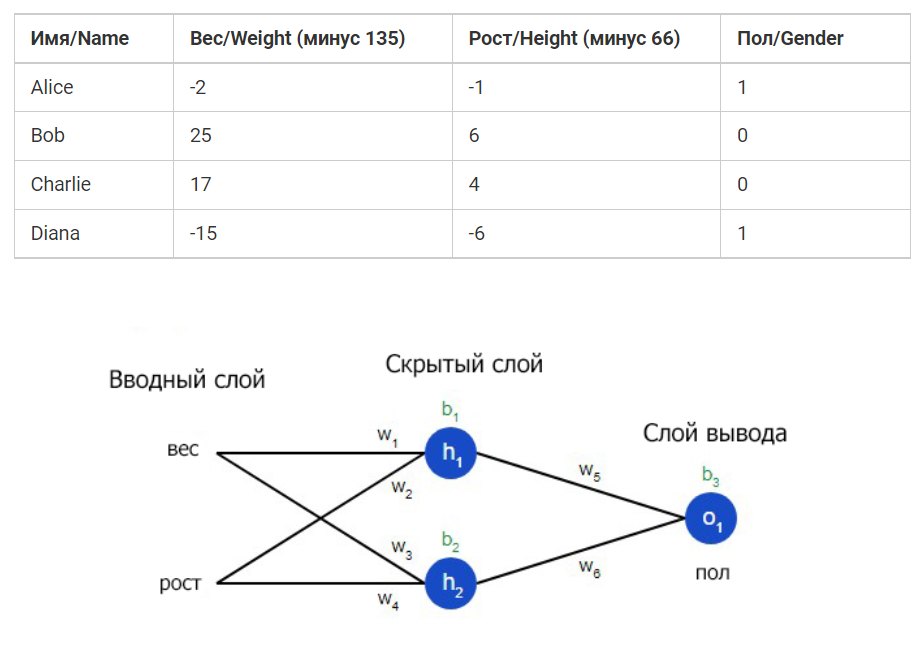
import numpy as np
def sigmoid(x):
# Функция активации sigmoid:: f(x) = 1 / (1 + e^(-x))
return 1 / (1 + np.exp(-x))
def deriv_sigmoid(x):
# Производная от sigmoid: f'(x) = f(x) * (1 - f(x))
fx = sigmoid(x)
return fx * (1 - fx)
def mse_loss(y_true, y_pred):
# y_true и y_pred являются массивами numpy с одинаковой длиной
return ((y_true - y_pred) ** 2).mean()
class OurNeuralNetwork:
"""
Нейронная сеть, у которой:
- 2 входа
- скрытый слой с двумя нейронами (h1, h2)
- слой вывода с одним нейроном (o1)
*** ВАЖНО ***:
Код ниже написан как простой, образовательный. НЕ оптимальный.
Настоящий код нейронной сети выглядит не так. НЕ ИСПОЛЬЗУЙТЕ этот код.
Вместо этого, прочитайте/запустите его, чтобы понять, как работает эта сеть.
"""
def __init__(self):
# Вес
self.w1 = np.random.normal()
self.w2 = np.random.normal()
self.w3 = np.random.normal()
self.w4 = np.random.normal()
self.w5 = np.random.normal()
self.w6 = np.random.normal()
# Смещения
self.b1 = np.random.normal()
self.b2 = np.random.normal()
self.b3 = np.random.normal()
def feedforward(self, x):
# x является массивом numpy с двумя элементами
h1 = sigmoid(self.w1 * x[0] + self.w2 * x[1] + self.b1)
h2 = sigmoid(self.w3 * x[0] + self.w4 * x[1] + self.b2)
o1 = sigmoid(self.w5 * h1 + self.w6 * h2 + self.b3)
return o1
def train(self, data, all_y_trues):
"""
- data is a (n x 2) numpy array, n = # of samples in the dataset.
- all_y_trues is a numpy array with n elements.
Elements in all_y_trues correspond to those in data.
"""
learn_rate = 0.1
epochs = 1000 # количество циклов во всём наборе данных
for epoch in range(epochs):
for x, y_true in zip(data, all_y_trues):
# --- Выполняем обратную связь (нам понадобятся эти значения в дальнейшем)
sum_h1 = self.w1 * x[0] + self.w2 * x[1] + self.b1
h1 = sigmoid(sum_h1)
sum_h2 = self.w3 * x[0] + self.w4 * x[1] + self.b2
h2 = sigmoid(sum_h2)
sum_o1 = self.w5 * h1 + self.w6 * h2 + self.b3
o1 = sigmoid(sum_o1)
y_pred = o1
# --- Подсчет частных производных
# --- Наименование: d_L_d_w1 представляет "частично L / частично w1"
d_L_d_ypred = -2 * (y_true - y_pred)
# Нейрон o1
d_ypred_d_w5 = h1 * deriv_sigmoid(sum_o1)
d_ypred_d_w6 = h2 * deriv_sigmoid(sum_o1)
d_ypred_d_b3 = deriv_sigmoid(sum_o1)
d_ypred_d_h1 = self.w5 * deriv_sigmoid(sum_o1)
d_ypred_d_h2 = self.w6 * deriv_sigmoid(sum_o1)
# Нейрон h1
d_h1_d_w1 = x[0] * deriv_sigmoid(sum_h1)
d_h1_d_w2 = x[1] * deriv_sigmoid(sum_h1)
d_h1_d_b1 = deriv_sigmoid(sum_h1)
# Нейрон h2
d_h2_d_w3 = x[0] * deriv_sigmoid(sum_h2)
d_h2_d_w4 = x[1] * deriv_sigmoid(sum_h2)
d_h2_d_b2 = deriv_sigmoid(sum_h2)
# --- Обновляем вес и смещения
# Нейрон h1
self.w1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w1
self.w2 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w2
self.b1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_b1
# Нейрон h2
self.w3 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w3
self.w4 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w4
self.b2 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_b2
# Нейрон o1
self.w5 -= learn_rate * d_L_d_ypred * d_ypred_d_w5
self.w6 -= learn_rate * d_L_d_ypred * d_ypred_d_w6
self.b3 -= learn_rate * d_L_d_ypred * d_ypred_d_b3
# --- Подсчитываем общую потерю в конце каждой фазы
if epoch % 10 == 0:
y_preds = np.apply_along_axis(self.feedforward, 1, data)
loss = mse_loss(all_y_trues, y_preds)
print("Epoch %d loss: %.3f" % (epoch, loss))
# Определение набора данных
data = np.array([
[-2, -1], # Alice
[25, 6], # Bob
[17, 4], # Charlie
[-15, -6], # Diana
])
all_y_trues = np.array([
1, # Alice
0, # Bob
0, # Charlie
1, # Diana
])
# Тренируем нашу нейронную сеть!
network = OurNeuralNetwork()
network.train(data, all_y_trues)
Обратите внимание, что этот код не самостоятельный. Вам необходимо его изучить, а запускать его нет смысла. Также этот код можно найти на Github.
Учитывайте то, что наши потери будут становиться постоянно меньше и меньше по ходу того, как наша нейросеть будет обучаться. Это изображено на графике.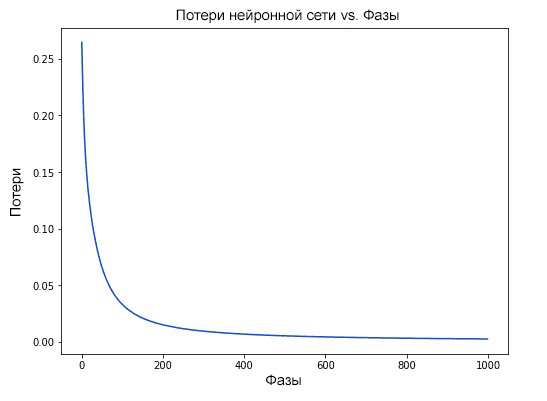
Теперь у нас есть возможность использовать нейросеть для того, чтобы предсказывать пол.
# Делаем предсказания
emily = np.array([-7, -3]) # 128 фунтов, 63 дюйма
frank = np.array([20, 2]) # 155 фунтов, 68 дюймов
print("Emily: %.3f" % network.feedforward(emily)) # 0.951 - F
print("Frank: %.3f" % network.feedforward(frank)) # 0.039 - M
Что по итогу?
Ура, результат достигнут. Он был получен следующим образом:
- Мы узнали, что такое нейроны и как правильно создаются блоки нейросетей.
- Была использована функция активации сигмоида в отношении нейронов.
- Мы увидели, что фактически нейронные сети – это лишь набор нейронов, которые связаны между собой.
- Создали набор с данными, которые содержат такие параметры, как рост, вес в качестве входящей информации (либо функций). Также в качестве вывода служил пол (который предсказывался на основе входящих данных).
- Узнали о функциях потерь и среднеквадратичной ошибке (MSE).
- Узнали, что тренировка нейросети фактически связана с минимизацией потерь. Именно этой цели и нужно добиться в процессе обучения искусственного интеллекта.
- Использовали обратное распространение для того, чтобы определять частные производные.
- Применяли стохастический градиентный спуск, чтобы осуществлять непосредственный тренинг нейронной сети.
Спасибо за внимание. Обязательно потренируйтесь, чтобы закрепить полученные знания на практике.
