Создание и тренировка Нейронной Сети с нуля в Python (пример) (Часть 1)

Создание нейронных сетей – это будущее. В этом ни у кого сомнений не остается. Поэтому каждый разработчик рано или поздно придет к этому. Сегодня мы рассмотрим то, как работают нейросети, а также то, как их можно реализовывать с помощью средств языка Python.

Несмотря на то, что это может показаться сложным для новичков, на деле ничего трудного нет. Слово «нейросети» нередко применяют в контексте чего-то сложного и непонятного обывателю. Тем не менее, все значительно легче для понимания.

Этот материал создан для тех людей, которые никогда прежде не работали с нейросетями и имеют поверхностное представление о них. Принцип работы нейросетей будет продемонстрирован на примере Python – одного из наиболее простых в изучении языков программирования.

Создание нейронных блоков

Сперва нужно определиться с тем, что собой являют нейроны. Это основные компоненты нейросети. Нейрон принимает входные данные, осуществляет определенные манипуляции, а потом выдает результат.

Искусственный нейрон – это математическая модель, которая выглядит таким образом.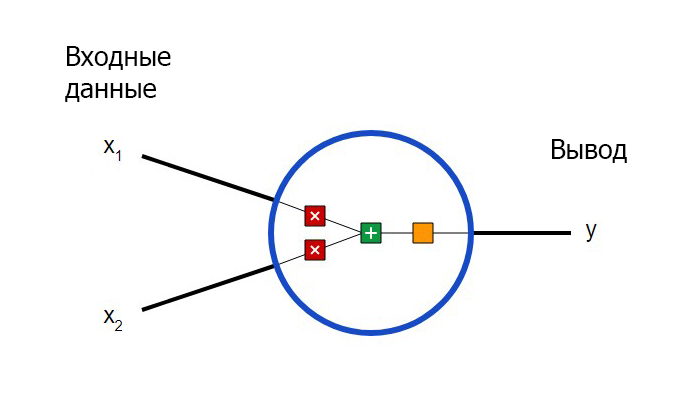

Здесь осуществляются три действия. Сначала каждый вход умножается на вес (красный цвет на схеме).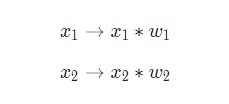

После этого каждый взвешенный вход складывается друг с другом со смещением b (зеленый цвет на схеме).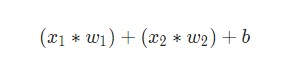

В результате, сумма передается через функцию активации (желтый цвет на схеме).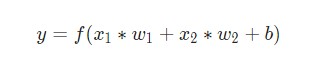

Функция активации нужна, чтобы подключать несвязанную входящую информацию с выводом. Форма очень простая и предсказуемая. Обычно в роли функции активации используется сигмоида. Но в ряде случаев может применяться и другая.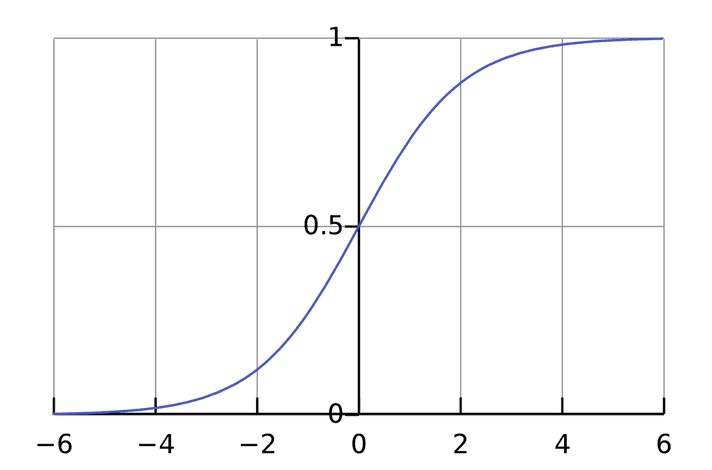

Она осуществляет вывод исключительно чисел, находящихся в определенных пределах (0,1). Это вполне может восприниматься, как компрессия от (−∞, +∞) до (0, 1). Большие отрицательные числовые значения становятся близкими к нулю, а большие числа положительной модальности становятся близкими к единице.

Пример нейросети

Допустим, у нас есть нейрон с двумя входами, задействующий стандартную функцию активации. У него параметры следующие.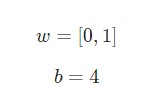

w = [0,1] – это лишь один из методов написания w1 = 0, w2 =1 в векторном представлении. Присвоим нейрону вход, значение x которого будет равняться [2,3]. Для большей компактности представления будем применять скалярное произведение.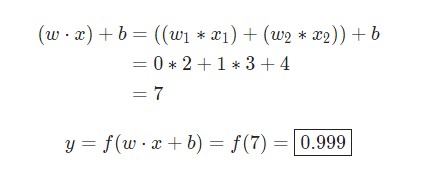

Учитывая то, что вход был x = [2,3], вывод будет равен 0,999. Вот и все. Подобный процесс передачи входных данных для получения вывода называется прямым распространением. Также можно встретить название feedforward.

Как создавать нейрон с нуля, используя средства Python?

Теперь давайте попробуем создать нейрон, воспользовавшись средствами Python. Для этого используется NumPy. Это высокопроизводительная библиотека для работы с числами. Она поддерживает целый спектр математических операций.

Давайте приведем пример кода, который показывает, как работает описанный ранее пример. 

import numpy as np

 

 

def sigmoid(x):

    # Наша функция активации: f(x) = 1 / (1 + e^(-x))

    return 1 / (1 + np.exp(-x))

 

 

class Neuron:

    def __init__(self, weights, bias):

        self.weights = weights

        self.bias = bias

 

    def feedforward(self, inputs):

        # Вводные данные о весе, добавление смещения 

        # и последующее использование функции активации

 

        total = np.dot(self.weights, inputs) + self.bias

        return sigmoid(total)

 

 

weights = np.array([0, 1])  # w1 = 0, w2 = 1

bias = 4  # b = 4

n = Neuron(weights, bias)

 

x = np.array([2, 3])  # x1 = 2, x2 = 3

print(n.feedforward(x))  # 0.9990889488055994

Обратите внимание, что после использования этого примера также будет выдан результат 0,999, как и в описанной нами ранее модели.

Пример создания сети из отдельных нейронов

Что такое нейронная сеть, по факту? Это совокупность искусственных нейронов, которые связаны друг с другом. Простая сеть может быть представлена в виде следующей модели.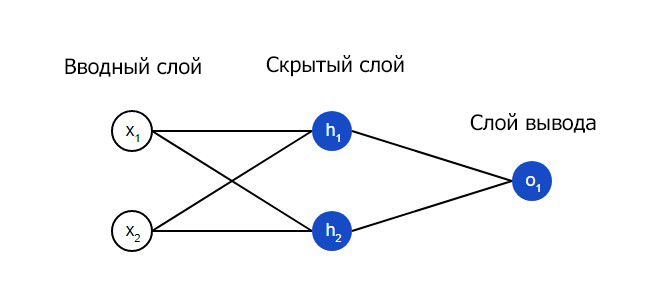

На входящем слое два входа – x1 и y1. На скрытом расположено два нейрона – h1 и h2. На слое вывода расположен один o1. Это также нейрон. Учтите, что входящая информация для последнего является результатами для h1, h2. Собственно, так и устроена работа нейросети.

То есть, скрытый слой, исходя из этой картинки, – это какой-угодно слой между вводным и слоем вывода, являющихся первым и последним слоями. Обратите внимание на то, что возможна ситуация, когда есть определенное количество скрытых слоев, и это нормально.

Прямое распространение

Теперь применим сеть, которая была показана ранее. Вообразим, что вес всех наших нейронов такой же самый: w = [0,1], а также такое же самое смещение b = 0. Помимо этого, в качестве функции активации используется сигмоида. h1,h2, o1 сами отметят итоги вывода нейронов, которые были ими представлены.

Что произойдет, если для ввода будет применяться x = [2,3]?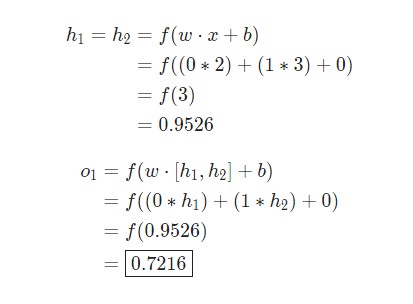

Результат нейросети для входящего значения x = [2,3] равняется 0,7216. Ничего сложного, как видим. 

Число слоев в нейросети может быть каким-угодно, равно как и число нейронов в них.

Суть не меняется: необходимо отправить входящую информацию через нейроны в сеть для получения определенных значений на выходе. Для того, чтобы было понятнее, как это реализовывать в Python, далее мы приведем код сети, которая была описана ранее.

Прямое распространение: создание нейронной сети этого типа

Теперь давайте рассмотрим то, как осуществить прямое распространение. В качестве точки опоры будет применяться такая модель.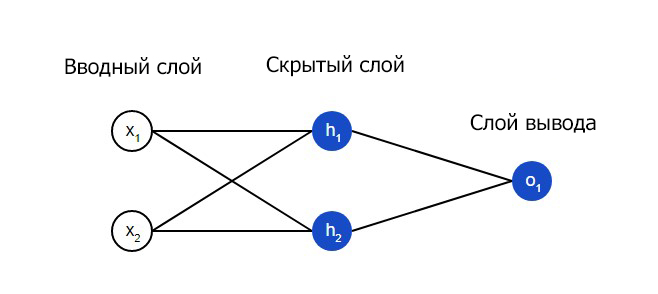

А вот фрагмент кода, который реализует данный функционал. 

import numpy as np

 

# ... Здесь код из предыдущего раздела

 

 

class OurNeuralNetwork:

    """

    Нейронная сеть, у которой: 

        - 2 входа

        - 1 скрытый слой с двумя нейронами (h1, h2) 

        - слой вывода с одним нейроном (o1)

    У каждого нейрона одинаковые вес и смещение:

        - w = [0, 1]

        - b = 0

    """

    def __init__(self):

        weights = np.array([0, 1])

        bias = 0

 

        # Класс Neuron из предыдущего раздела

        self.h1 = Neuron(weights, bias)

        self.h2 = Neuron(weights, bias)

        self.o1 = Neuron(weights, bias)

 

    def feedforward(self, x):

        out_h1 = self.h1.feedforward(x)

        out_h2 = self.h2.feedforward(x)

 

        # Вводы для о1 являются выводами h1 и h2

        out_o1 = self.o1.feedforward(np.array([out_h1, out_h2]))

 

        return out_o1

 

 

network = OurNeuralNetwork()

x = np.array([2, 3])

print(network.feedforward(x))  # 0.7216325609518421

У нас снова был получен результат 0,7216. Видим, что все успешно работает.

Вариант обучения нейросети – минимизация потерь, часть 1

Допустим, мы имеем такие параметры.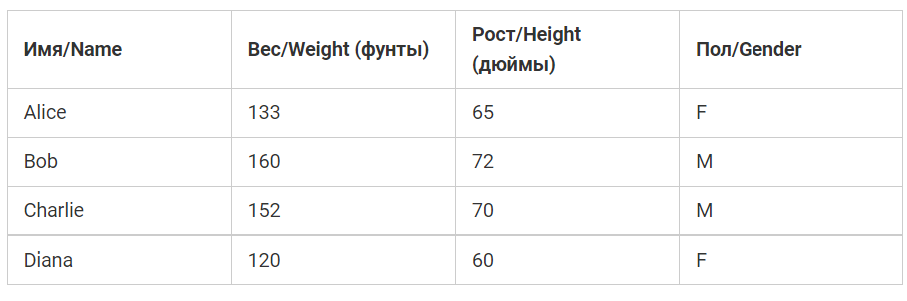

Давайте обучим нейросеть так, чтобы она угадывала пол человека в зависимости от его параметров.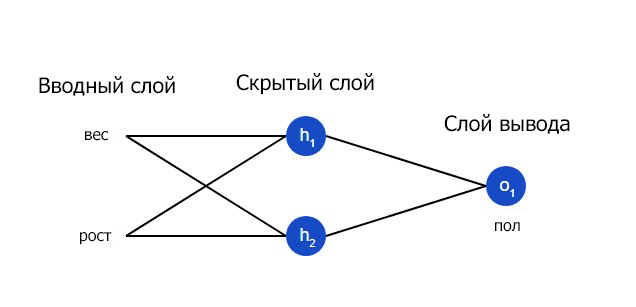

Male будут нулем, а Female единицей. Чтобы представление упростить, будут определенные смещения.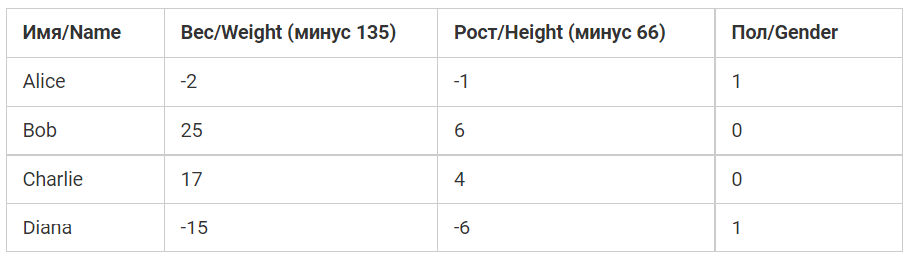

Для достижения оптимизационных целей здесь выполнены смещения 135 и 66. Тем не менее, в большинстве случаев используются усредненные значения.

Потери

Перед тренировкой нейросети надо выбрать метод оценки того, хорошо ли она работает. Это нужно, чтобы в последующем задача ею выполнялась лучше. Это принцип потери.

В этом примере будем использовать среднеквадратическую ошибку.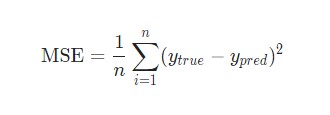

Давайте разберем это.

• n – это количество элементов, которые рассматриваются. В нашем примере оно равняется 4. Это Alice, Bob, Charlie, Diana.

• y – переменные, которые наша нейронная сеть должна прогнозировать. В нашем примере это пол.

• ytrue – реальная величина переменной. Проще говоря, верный ответ. Так, для Alice ytrue равняется 1. То есть, женский пол.

• ypred – это переменная, в которой будет храниться предсказание касаемо пола человека. Это результирующий вывод нейросети.

(ytrue – ypred)^2 называется квадратичной ошибкой. В этой ситуации функция потери фактически берет усредненное число по всем квадратичным ошибкам. Собственно, по этой причине и название такое. Чем качественные прогноз, тем такие потери меньше.

Задача тренировки нейросети и заключается в том, чтобы максимально уменьшить потери.

Пример подсчета потерь в нейросети

Допустим, нейросеть в каждом случае выводит значение 0. Проще говоря, она считает, что все люди – это мужчины. Какая потеря в этом случае?

Код расчета потерь в Python

Давайте приведем пример кода, который будет рассчитывать среднеквадратическую ошибку 

import numpy as np

 

 

def mse_loss(y_true, y_pred):

    # y_true и y_pred являются массивами numpy с одинаковой длиной

    return ((y_true - y_pred) ** 2).mean()

 

 

y_true = np.array([1, 0, 0, 1])

y_pred = np.array([0, 0, 0, 0])

 

print(mse_loss(y_true, y_pred))  # 0.5

Если появляются трудности с пониманием работы кода, необходимо ознакомиться с quickstart в NumPy для операций с массивами.

Многовариантные исчисления, часть 2

Теперь задача понятна – минимизация потерь нейросети. Уже сейчас стало понятно, что влияние на предсказания нейросети возможно с помощью изменения таких параметров, как смещение и вес. Тем не менее, что делать для уменьшения потерь?

Сейчас будет рассмотрена тема многовариантных исчислений. Если вам она не знакома, то части с математическими вычислениями можно просто пропустить.

Для того, чтобы было проще понять, давайте вообразим, что в наборе с данными рассматривается исключительно Alice.

После этого, потеря среднеквадратической ошибки станет квадратической ошибкой для Alice.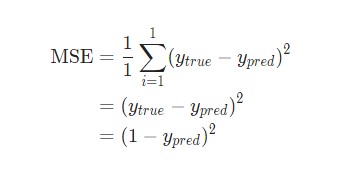

Есть еще метод, как лучше понять потери. Для этого необходимо ее представить в виде функции веса и смещения. Давайте обозначим каждый вес и смещение в сети, которая нами рассматривается.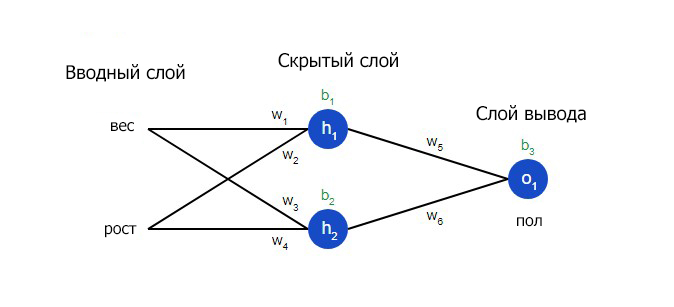

Затем возможно прописать потерю в качестве многовариантной функции.

Допустим, нам необходимо подредактировать w1. Как же тогда изменится потеря L после того, как такие коррективы будут осуществлены?

Чтобы получить ответ на этот вопрос, может пригодиться частная производная dL/dw1. Как же она определяется?

Тут вычисления будут довольно непростыми. Поэтому рекомендуется прочитать этот фрагмент несколько раз, чтобы лучше его понять. Также рекомендуется делать заметки, поскольку они могут пригодиться в дальнейшем.

Сперва, перепишем частную производную в контексте

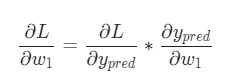
В целом, такие расчеты выполнимы благодаря дифференцированию сложной функции.

Определить  можно с помощью определенной выше L = (1 — ypred)^2: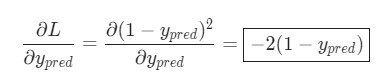

Давайте поймем, как поступать с Как и прежде, позволим h1, h2, o1 стать результатами вывода нейронов, которые они представляют. Далее выполняются такие расчеты.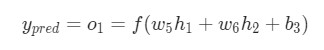

Поскольку w1 влияет исключительно на h1, а не на h2, можно представить это в виде следующей записи.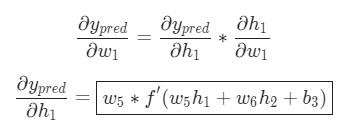

Аналогичные действия выполняются для

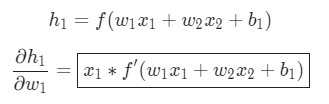
Здесь x1 – вес, а x2 – рост. В этом примере f`(x) в качестве производной функции сигмоида встречается уже во второй раз. Давайте сделаем попытку вывести ее.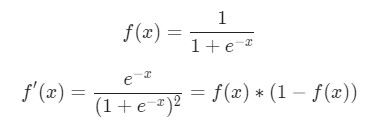

Функция, описанная в данном примере, будет использоваться чуть-чуть позднее.

Вот и все. Теперь  разделена на несколько составляющих, которые будут оптимальными для произведения расчетов.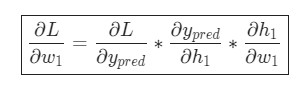

Это система определения частных производных при работе в обратном порядке известна, как метод обратного распространения ошибок.

Итак, у нас появилось большое количество формул. В них запутаться очень просто. Мы подробно разберем принцип их работы в следующей части этого обучающего материала.