Как вычислить среднее арифметическое в Excel

Вычисление среднего арифметического числа – довольно частая процедура, которую приходится делать пользователям Excel. Существует сразу несколько возможных методов, позволяющих это сделать в самых разных ситуациях, в том числе, и использование статистических функций. Давайте более детально разберемся, что делать для вычисления среднего арифметического числа в Excel?

Как найти среднее арифметическое чисел (математика)?

Чтобы определить среднее арифметическое нескольких чисел или ячеек, надо взять все значения в последовательности, выполнить между ними операцию сложения, а полученный результат разделить на их общее количество. Очень легко показать работу среднего арифметического на примере школьных отметок в табеле, поскольку показатель среднего балла знакомый каждому, кто учился в заведении среднего образования.

Предположим, у нас есть итоговая таблица, в которой приводятся оценки одного ученика за выполненные промежуточные контрольные работы: 3, 4, 3, 5, 5. Средним значением за четверть в этом случае будет 4 балла.

Среднее арифметическое Excel

Допустим, у нас есть таблица с набором определенных значений. Что они обозначают, не так важно в этой ситуации. Пусть это будет случайный набор цифр. Это никак не повлияет на логику рассуждения.

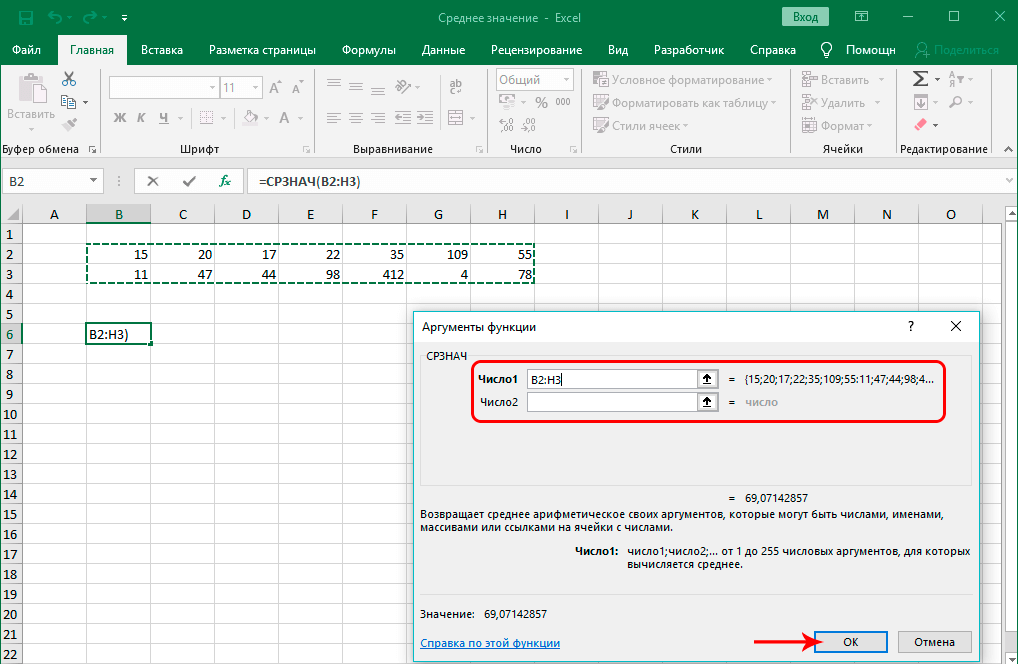
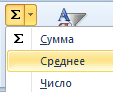
Нам необходимо нажать левой клавишей мыши по ячейке A2, тем самым активировав ее. После этого переходим в главное меню или обращаем внимание на ленту, находим там опцию «Редактирование», и в появившемся меню делаем левый клик мыши по кнопке «Сумма». При этом клик осуществляем не по самому значку, а по стрелочке, располагающейся рядом с ним. После этого появится еще одно меню, в котором будет набор разных функций. В нашем случае нас интересует «Среднее». После того, как нажать по ней, в выделенной ячейке будет автоматически записана формула.

Это еще не все. После этого нужно ввести аргумент функции, для чего достаточно просто выделить те ячейки, для которых и требуется определение среднего арифметического. После этого нажимаем клавишу «Enter».

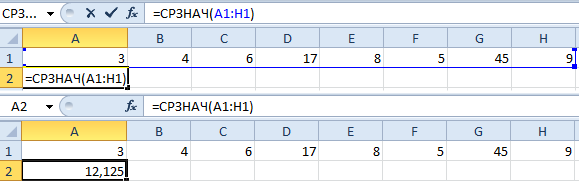
Синтаксис СРЗНАЧ

Как видим, нами используется формула СРЗНАЧ, которая имеет свой синтаксис. Он очень простой. Сначала пишется знак равно, как и с любой другой функцией. После этого пишется название СРЗНАЧ, после чего открывается скобка и записывается один единственный аргумент – диапазон значений, из которых требуется получить среднее арифметическое. После этого закрывается скобка.

Аргументы СРЗНАЧ

На практике формула вместе с введенным аргументом будет выглядеть следующим образом.

=СРЗНАЧ(A1:A10).

Такая формула осуществит расчет суммы значений от первого до десятого ряда, после чего поделит получившийся результат на 10. 

Вычисление среднего арифметического с помощью Мастера функций

Мастер функций – это универсальная возможность Excel, позволяющая осуществлять самые сложные расчеты, при этом не зная названий формул. Достаточно просто выбрать правильную из списка, а потом вести правильные аргументы. Причем все они показываются в отдельном диалоговом окне с подсказками. Так что пользователь легко может разобраться, какая функция за что отвечает и какой она имеет синтаксис.

Рекомендуется поиграться с этим перечнем на досуге, чтобы получить представление о том, какие функции Excel были заложены разработчиками.

Чтобы вызвать мастер функций, необходимо нажать комбинацию клавиш Shift + F3 или найти возле строки ввода формул клавишу fx. После того, как это сделать, появится окошко, в котором нам нужно найти функцию «СРЗНАЧ». Значительно проще искать нужную нам функцию, если выбрать ее тип. В специальном выпадающем меню, расположенном в верхней части экрана, нужно выбрать пункт: «Статистические». Тогда перечень существенно сузится и будет проще выбирать.

Потом появится еще одно окно, в котором можно осуществить ввод аргументов функции СРЗНАЧ.

Частный вариант – вызов функции вывода среднего арифметического из ленты. Для этого надо найти вкладку «Формулы», потом перейти в раздел «Другие функции», там навести мышью на пункт «Статистические». После всех этих операций появится функция СРЗНАЧ.

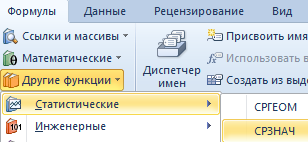
Панель формул

Каждый документ содержит панель формул, которая меняется в зависимости от того, какую ячейку выбрать. Если формула там есть, то она там будет записана. Если формула отсутствует, то там тогда будет отображаться просто значение ячейки (например, если там записан просто текст). На этом скриншоте видно конкретный пример, как может использоваться строка ввода формул. С ее помощью можно посмотреть на то, какая формула кроется за определенным числом (13,2) на примере, а также отредактировать аргументы. Или вообще убрать старую формулу и ввести новую. Или убрать все формулы, а оставить пустое значение или число. Возможностей у нее много достаточно. Можно выбрать любую, которая поможет выполнить поставленную задачу.

Ручной ввод функций

Функция СРЗНАЧ относится к простым. Ее легко запомнить, а также она содержит всего один аргумент. Поэтому мы ее введем вручную. В качестве примера будем использовать скриншот, приведенный выше. Как видим, можно использовать два разрозненных диапазона, не соединенных непосредственно между собой. 

Мы введем ее вручную.

=СРЗНАЧ(A1:B1;F1:H1)

Очевидно, что в соответствующих местах нужно выставлять свои адреса. Если нужно, чтобы при копировании в другие ячейки они сохранялись, не стоит забывать делать ссылки абсолютными. Для этого их нужно выделять, а потом нажимать кнопку F4.

Настоятельно рекомендуется запоминать все функции, которые изучаете, потому что в будущем это позволит очень сильно сэкономить время. 

Расчет среднего значения по условию

Может понадобиться находить среднее значение для определенных чисел только при условии, что они соответствуют конкретному критерию. Условие может быть любым, как текстовым, так и числовым. Также она может записываться как непосредственно в формулу, так и в другие ячейки.

Можно, конечно, использовать функцию ЕСЛИ в сочетании с функцией СРЗНАЧ, но это немного тяжеловатая задача. Если приходится эту комбинацию использовать очень часто, на это всё требуется много времени. Значительно разумнее использовать функцию СРЗНАЧЕСЛИ. В ней в разных ситуациях используется два или три аргумента, но их водить всё равно быстрее, чем прописывать две разные функции в одну формулу.

Представим такую ситуацию: нам руководство поставило задачу определить среднее арифметическое для тех значений, которые равняются или больше 10. 

Конечная формула будет следующей:

 =СРЗНАЧЕСЛИ(A1:A8;»>=10″)

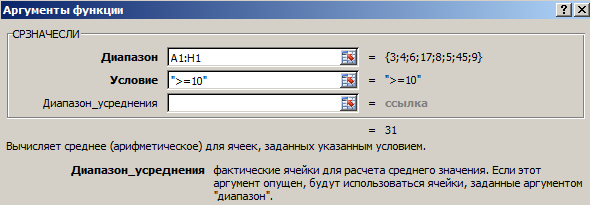
В результате, получится такое значение.

Разберем аргументы этой функции более подробно.

1. Диапазон. Это непосредственно тот диапазон, в котором будет содержаться набор критериев.
2. Условие. Это непосредственно условие. То есть, значение должно как-то соотноситься с критерием. В нашем случае оно должно быть больше или равно 10.
3. Диапазон усреднения. Необязательный аргумент, который используется если значения, для которых нужно искать среднее арифметическое, находятся в другом месте, а не непосредственно являются критериями. 

Мы опустили третий пункт, потому что в первом аргументе диапазон числовой, в то время как его лучше использовать лишь при текстовых критериях там.

Как найти среднее значение с учетом текста?

Если есть такая необходимость, критерий может быть записан в какой-то ячейке, а дальше просто достаточно дать ссылку на нее. 

Теперь давайте отыщем среднее арифметическое, используя в качестве диапазона критерия набор текстовых значений из колонки А.

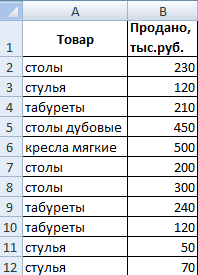
Внешний вид функции будет следующим: =СРЗНАЧЕСЛИ($A$2:$A$12;A7;$B$2:$B$12). В качестве диапазона здесь используется соответствующий столбец (ссылки закреплены на случай, если нужно будет копировать), а критерием поиска будет выступать адрес ячейки, содержащей слово «столы» (или же можно просто написать это слово в соответствующем месте). А в качестве диапазона усреднения мы здесь использовали колонку B.

Важно! Указание диапазона усреднения является обязательным требованием к текстовым критериям.

Как рассчитать средневзвешенную цену в Excel?

Чтобы определить средневзвешенную цену, необходимо использовать функции СУММПРОИЗВ и СУММ. Итак, у нас есть лист, описывающий разные виды товаров, их количество и стоимость.

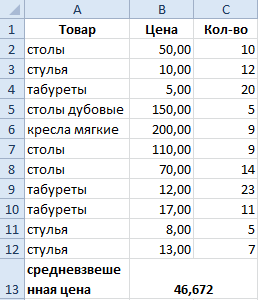
Чтобы узнать средневзвешенную цену в этом случае, необходимо использовать формулу.

=СУММПРОИЗВ(C2:C12;B2:B12)/СУММ(C2:C12).

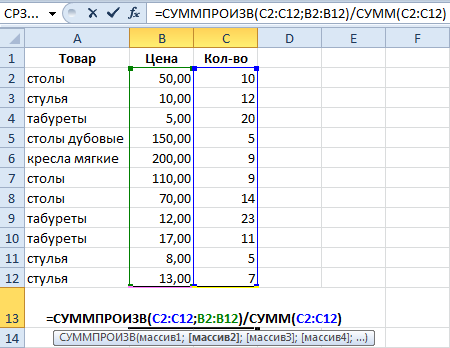
Эта формула работает в два этапа. Функция СУММПРОИЗВ позволяет определить общую сумму денег, которую получилось заработать компании после того, как все товары были проданы. А далее используется функция СУММ, которая просто определяет общее количество проданных товаров.

Далее происходит операция деления общей выручки товара на количество единиц. Вот таким образом и получилось найти средневзвешенную стоимость – показатель, который определяет то, насколько значимым оказывается конкретный товар в общей выручке.

Среднее квадратическое отклонение: формула в Excel

Когда заходить речь о среднем арифметическом, обязательно где-то рядом находится еще одно понятие – среднеквадратическое отклонение (или просто стандартное отклонение). Но чтобы понять, что это такое, необходимо сначала разобраться, что такое дисперсия.

Этот термин означает степень разброса значений. Все-таки разница между набором значений 4 и 6 со средним арифметическим 5 и 1 и 9 с тем же средним значением колоссальна. В первом случае дисперсия минимальная, а во втором значения находятся в очень большом разбросе.

Формула расчета дисперсии довольно сложная, но ее можно легко рассчитать с помощью стандартных инструментов Excel. Для этого есть две функции: ДИСП.В и ДИСП.Г

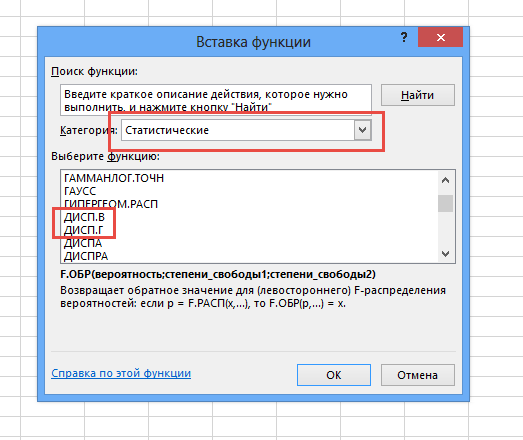
На практике это значение само по себе используется редко. Оно может применять для проверки правильности статистической гипотезы или определения коэффициентов корреляции. В разрезе нашей статьи дисперсия используется для определения среднеквадратического отклонения, которое образуется по простой формуле. Нужно из полученного значения дисперсии извлечь квадратный корень. 

Есть два вида стандартного отклонения в Excel – по генеральной совокупности и выборочной.

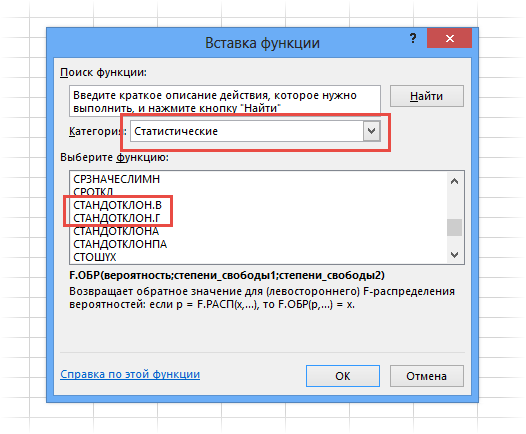
Формула дисперсии нам не нужна для расчета стандартного отклонения (за тем лишь исключением, если по каким-то причинам она уже известна, тогда можно просто извлечь из нее корень). Как видим из скриншота выше, есть две формулы стандартного отклонения в Excel.

Здесь, как видим, нужно разобраться еще в двух терминах: генеральная и выборочная совокупность. Первый – это весь диапазон анализируемых данных (общество, например), а второй – это часть этого диапазона, которая должна представлять генеральную совокупность (например, конкретная группа людей, которая соответствует ей по демографическим, социально-экономическим показателям).

Для стандартного отклонения характерна привязка к масштабу данных. Чтобы получить полное представление о том, насколько сильный разброс значений, наличия одних лишь абсолютных значений недостаточно. Необходимо еще получить относительные.

Для этого используется коэффициент вариации. Чтобы его вычислить, необходимо разделить стандартное отклонение на среднее значение. Его можно использовать, если значение не равно нулю и он оказывается полезным в тех ситуациях, когда имея информацию о среднем значении, можно понимать, насколько сильно отклонение. 

Таким образом, получение среднего арифметического в Excel может осуществляться целым рядом способов. Это одна из самых главных формул, используемых в электронных таблицах. Поэтому ее знать обязательно наизусть. Тем более, что запомнить ее несложно, название интуитивно понятное, а аргумент всего один (хотя если нужно проанализировать несколько диапазонов, то количество параметров будет большим).