«Поиск решения» является надстройкой Эксель, посредством которой возможно подобрать лучшее решение задач на основе указанных ограничений. Функция дает возможность составлять график работников, распределять расходы либо инвестиционные вложения. Знание принципа работы такой функции поможет сэкономить время и силы.
Что такое Поиск решений
В комплексе с различными другими опциями в Excel существует одна менее популярная, однако крайне нужная функция «Поиск решения». Невзирая на то, что отыскать ее бывает нелегко, ознакомление с ней и использование помогает в разрешении множества задач. Опция обрабатывает данные и выдает оптимальное решение из допустимых. В статье описывается, как непосредственно функционирует «Поиск решения».
Как включить функцию «Поиск решения»
Невзирая на эффективность, рассматриваемая опция не находится на видном месте панели инструментов либо контекстного меню. Большинство юзеров, которые работают в Эксель, не знают о ее наличии. По умолчанию такая функция выключена, для ее отображения следует произвести такие действия:
- Открываем «Файл», нажимая на соответствующее название.
- Кликаем на раздел «Параметры».
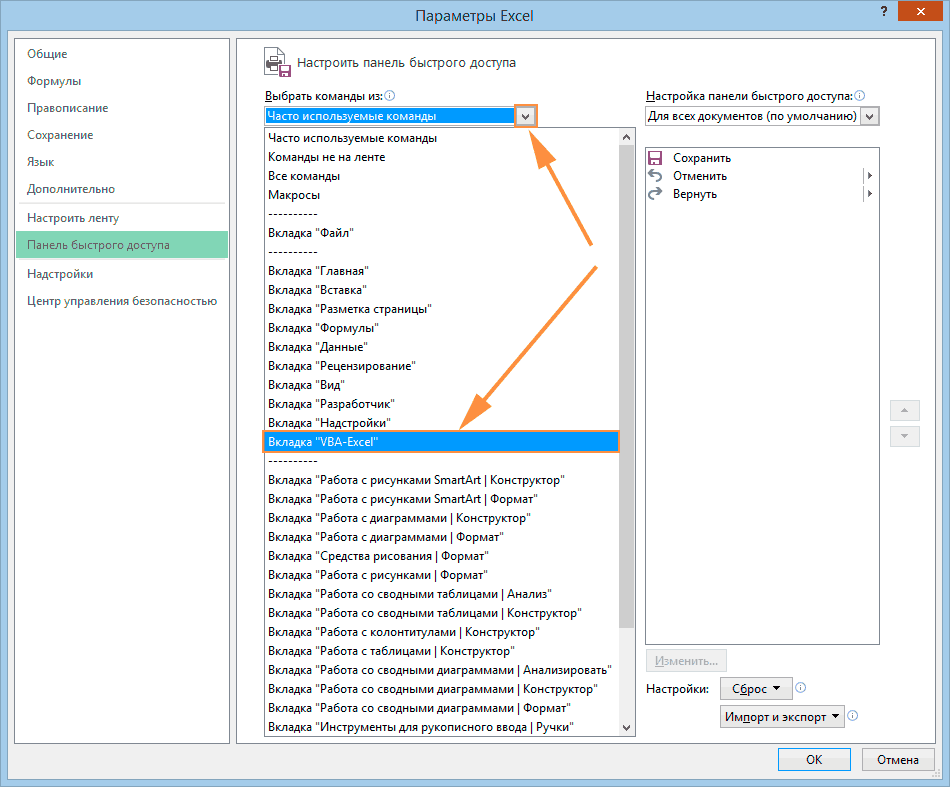
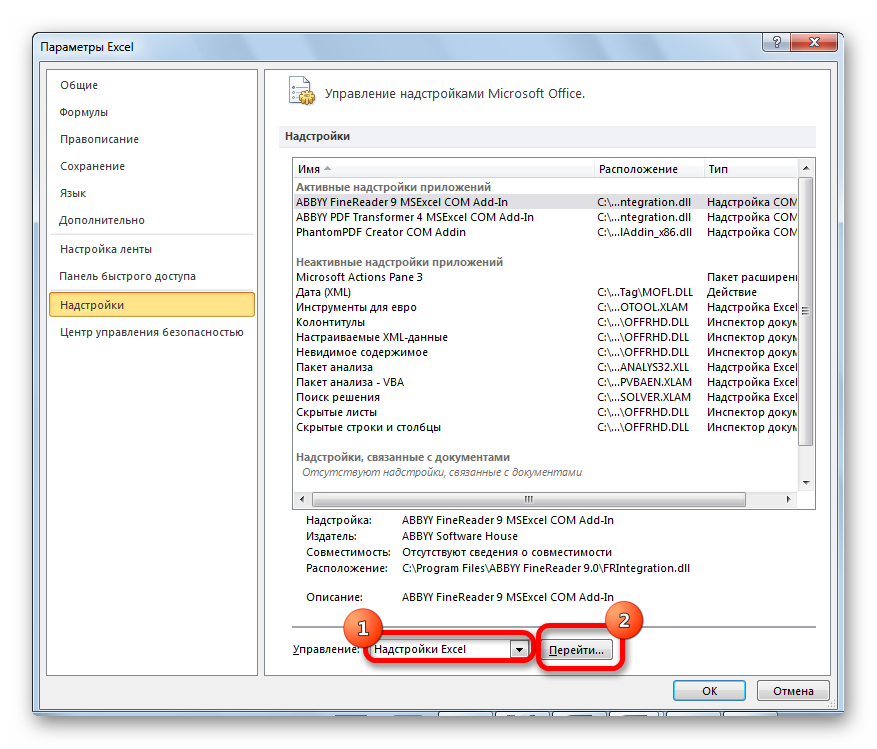
- Затем выбираем подраздел «Надстройки». Тут будут отображены все надстройки программы, внизу появится надпись «Управление». С правой стороны от нее будет всплывающее меню, где следует выбрать «Надстройки Excel». Потом нажимаем «Перейти».
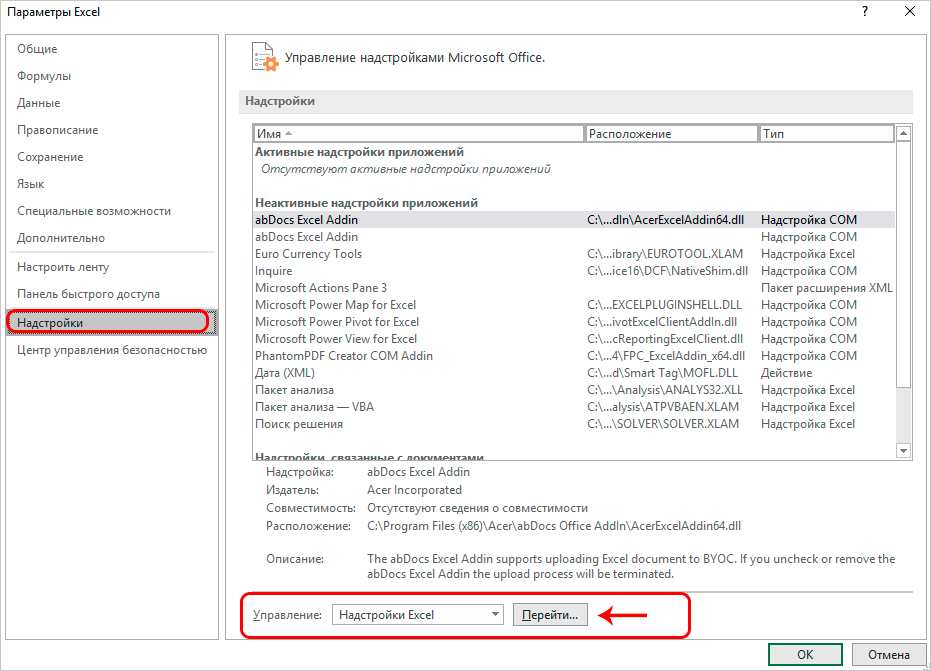
1 - На мониторе высветится дополнительное окно «Надстройки». Устанавливаем флажок возле искомой функции и кликаем «ОК».
- Нужная функция появится на ленте справа от раздела «Данные».
О моделях
Данная информация будет крайне полезна тем, кто лишь ознакамливается с понятием «оптимизационная модель». До того, как воспользоваться «Поиском решения», рекомендуется исследовать материалы о методах построения моделей:
- рассматриваемая опция даст возможность выявить оптимальный метод, чтобы осуществить выделение средств на вложения, загрузку помещения, поставку товаров либо иные действия, где необходимо отыскать оптимальный вариант решения.
- «Оптимальный метод» в такой ситуации будет означать: увеличение доходов, снижение трат, улучшение качества и др.
Типовые задачи по оптимизации:
- Определение плана производства, во время чего прибыль от продажи выпущенных товаров будет максимальной.
- Определение карт перевозок, во время чего траты на транспортировку минимализируются.
- Поиск распределения нескольких станков по различным видам работ, чтобы траты на производство были снижены.
- Определение наименьшего срока выполнения работ.
Важно! Чтобы формализовать поставленную задачу, необходимо создать модель, отражавшую основные параметры предметной области. В Эксель модель является комплексом формул, использующих переменные. Рассматриваемая опция подыскивает такие показатели, чтобы целевая функция была больше (меньше) либо равнялась указанному значению.
Подготовительный этап
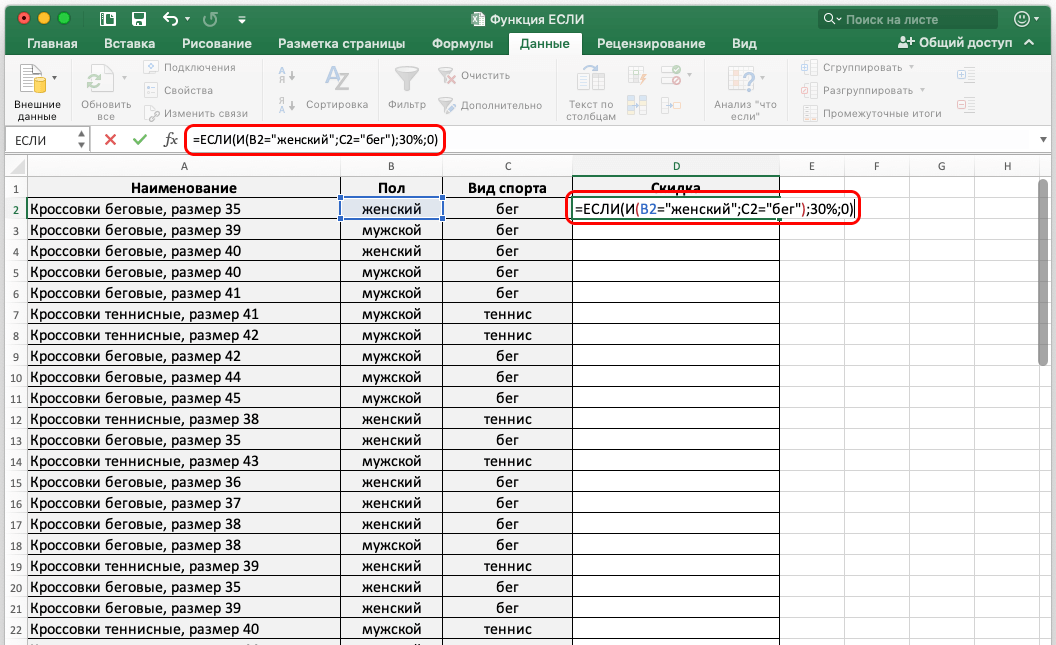
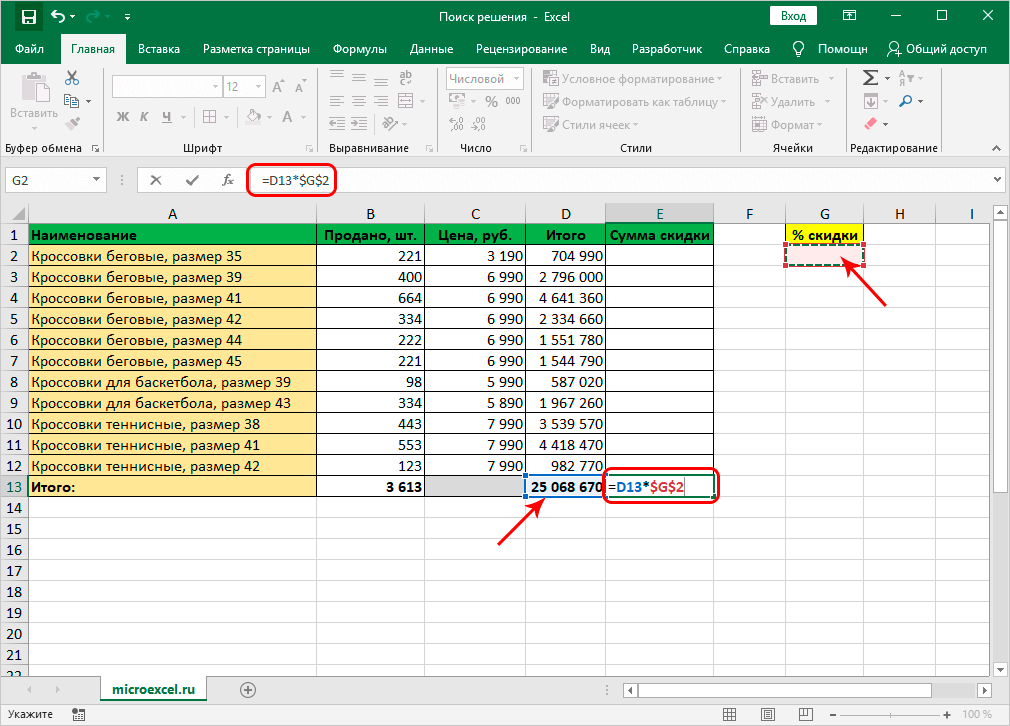
Перед тем как разместить функцию на ленте, необходимо изучить принцип функционирования опции. К примеру, есть сведения по реализации товаров, указанные в таблице. Задачей является назначение для каждого наименования скидки, которая составляла бы 4.5 млн. рублей. Параметр отображается внутри ячейки, именуемой целевой. Отталкиваясь от нее, рассчитываются прочие параметры.
Нашей задачей станет вычисление скидки, на которую умножаются суммы по реализации различной продукции. Эти 2 элемента связываются формулой, прописываемой так: =D13*$G$2. Где в D13 прописывается суммарное количество по реализации, а $G$2 – адрес искомого элемента.
Применение функции и ее настройка
Когда формула будет готова, необходимо использовать непосредственно саму функцию:
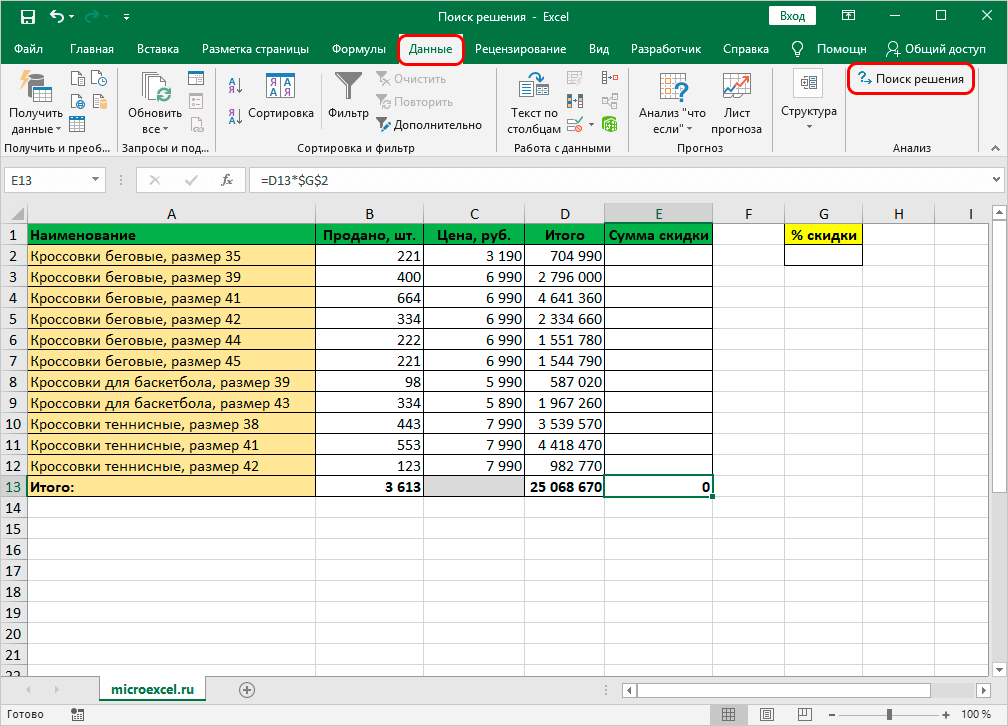
- Нужно переключиться в раздел «Данные» и нажать «Поиск решения».
- Откроются «Параметры», где задаются требуемые настройки. В строке «Оптимизировать целевую функцию:» следует указать ячейку, где выводится сумма по скидкам. Есть возможность прописать координаты самостоятельно или выбрать из документа.
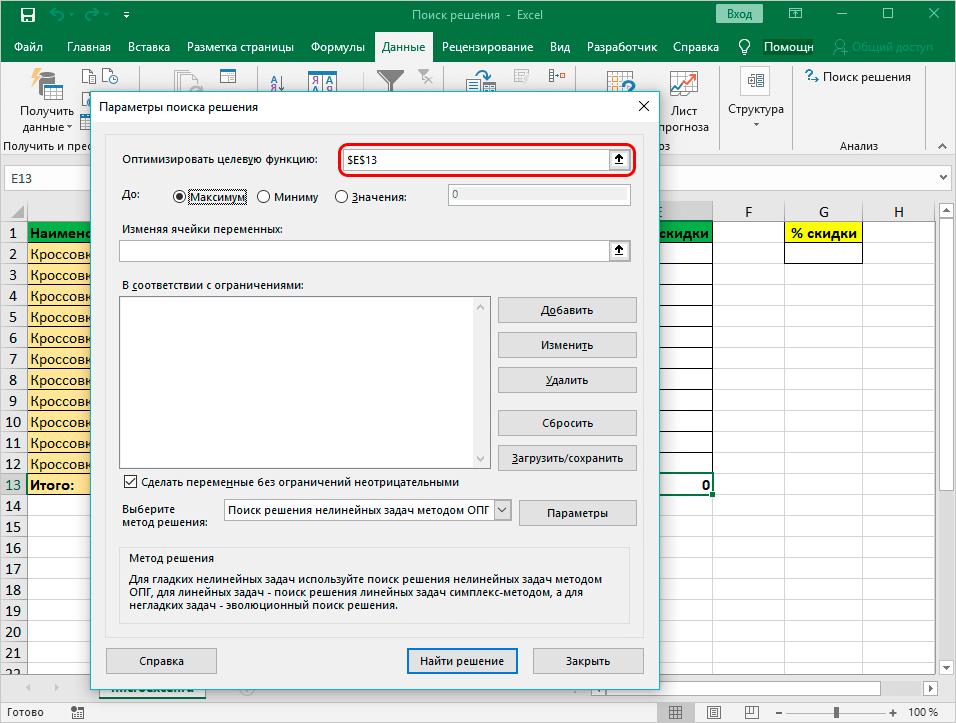
- Далее нужно перейти к настройкам прочих параметров. В разделе «До:» есть возможность задать максимальную и минимальную границу либо точное число.
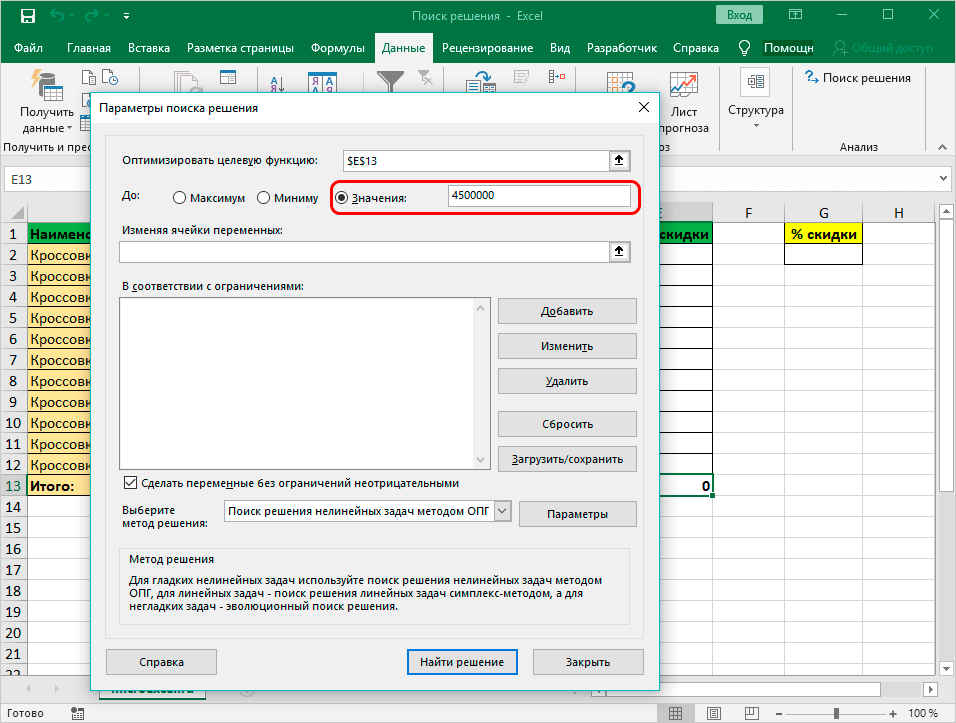
- Потом заполняется поле «Изменяя значения переменных:». Здесь вносятся данные искомой ячейки, которая содержит конкретное значение. Координаты прописываются самостоятельно или кликается соответствующая ячейка в документе.
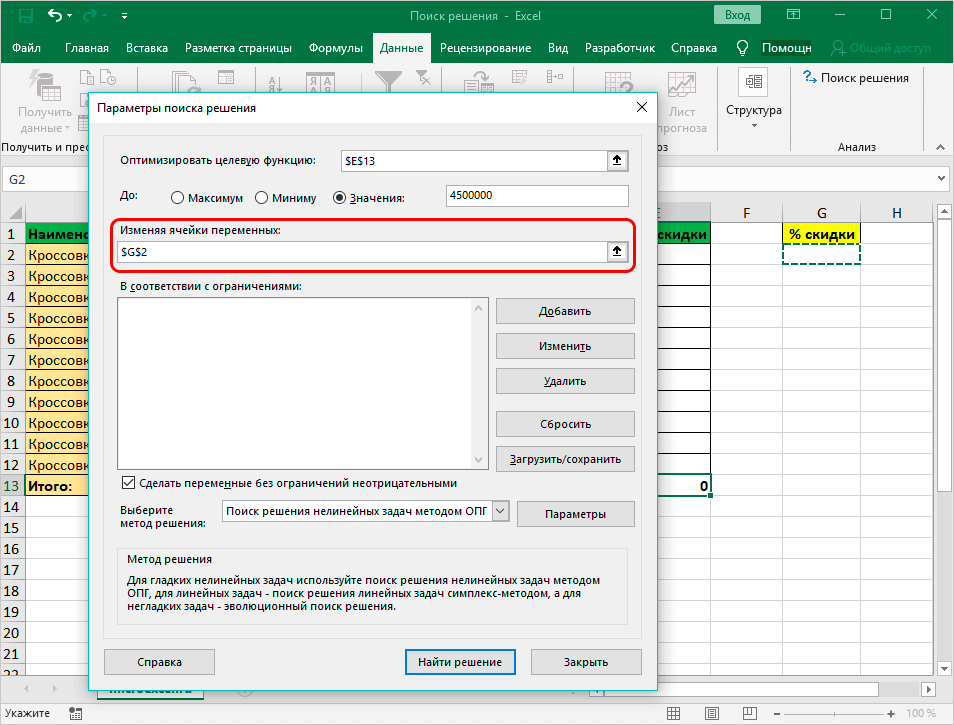
- Затем редактируется вкладка «В соответствии с ограничениями:», где задаются ограничения применяемых данных. К примеру, исключаются десятичные дроби либо отрицательные числа.
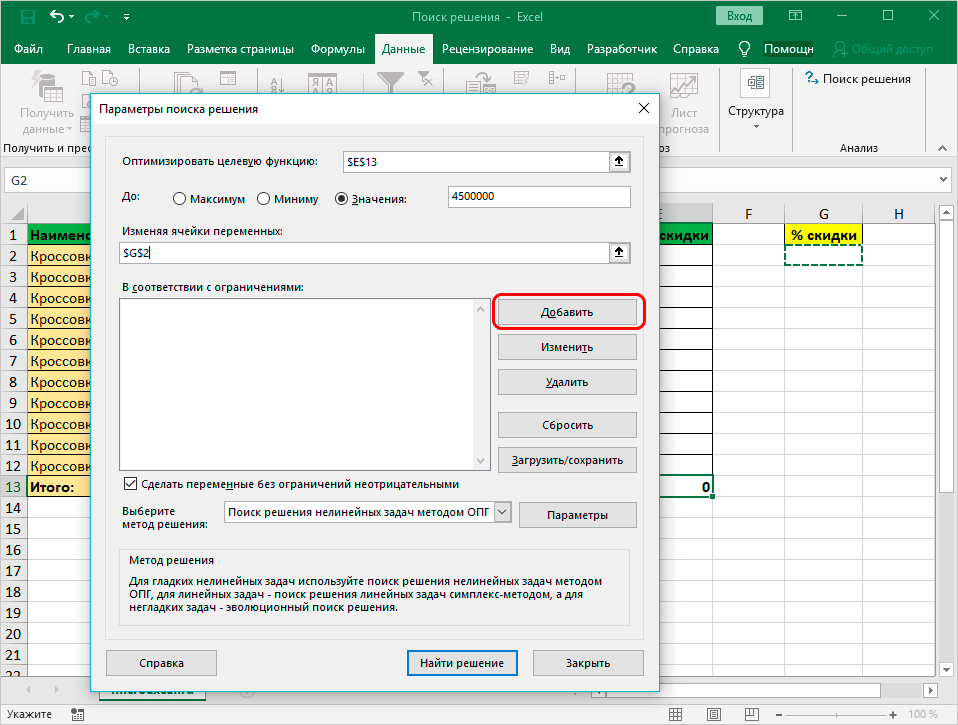
- После открывается окно, которое позволяет добавлять ограничения при расчетах. В начальной строке указываются координаты ячейки либо целого диапазона. Следуя условиям задачи, указываются данные искомой ячейки, где выводится показатель скидки. Затем определяется знак сравнения. Устанавливается «больше либо равно», чтобы конечное значение не было со знаком «минус». «Ограничение», устанавливаемое в 3 строке, в такой ситуации равняется 0. Возможно выставить также ограничение посредством «Добавить». Последующие действия аналогичны.
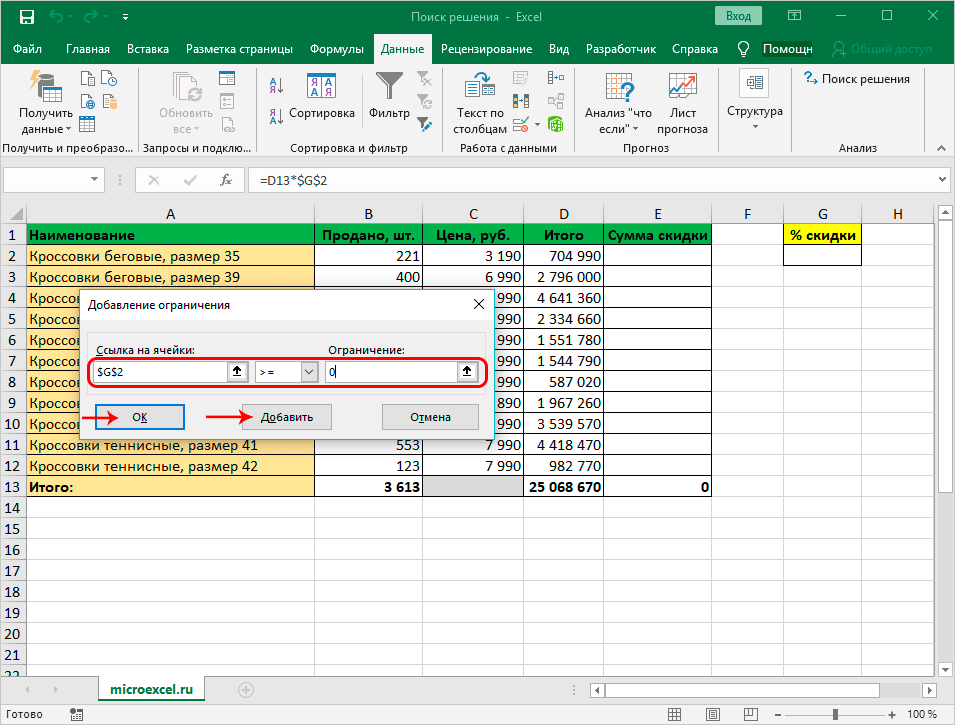
- Когда выполнены вышеописанные действия, в самой большой строке появляется установленное ограничение. Перечень бывает большим и будет зависеть от сложности расчетов, однако в конкретной ситуации достаточно 1 условия.
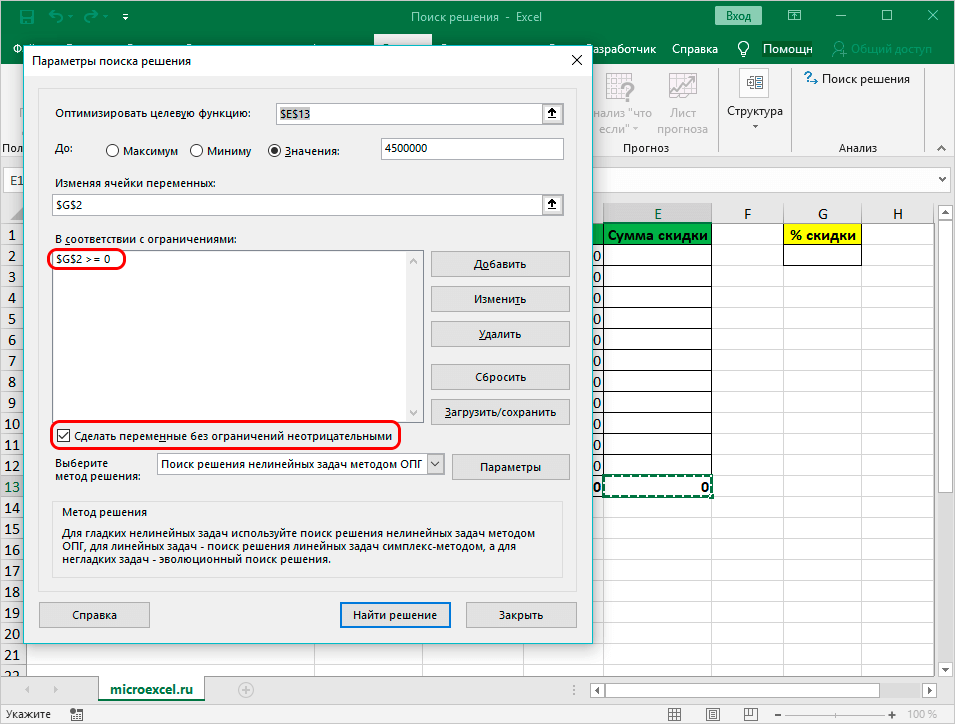
- Кроме того, возможно выбирать другие дополнительные настройки. Внизу с правой стороны присутствует опция «Параметры», которая позволяет это сделать.
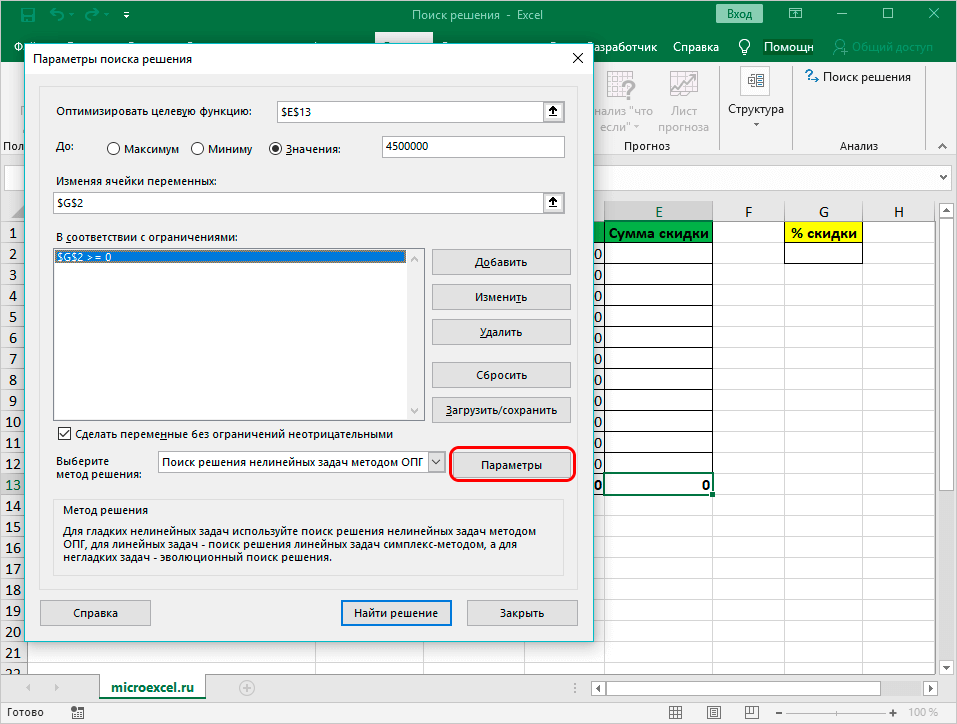
- В настройках можно выставить «Точность ограничения» и «Пределы решения». В нашей ситуации использовать эти опции нет нужды.
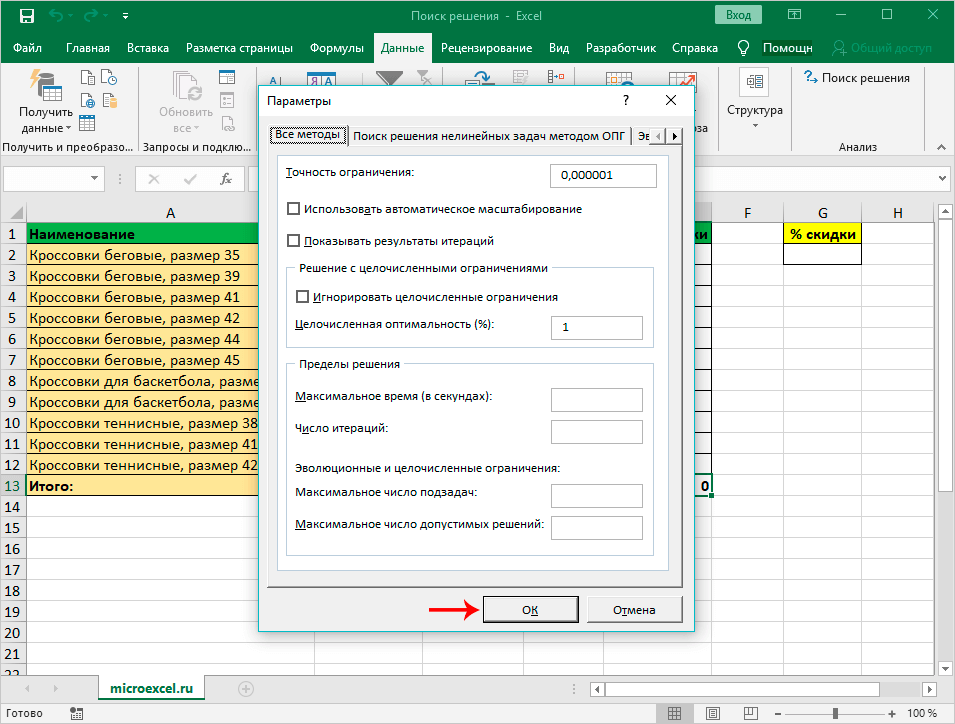
- Когда настройки завершены, запускается сама функция – нажимается «Найти решение».
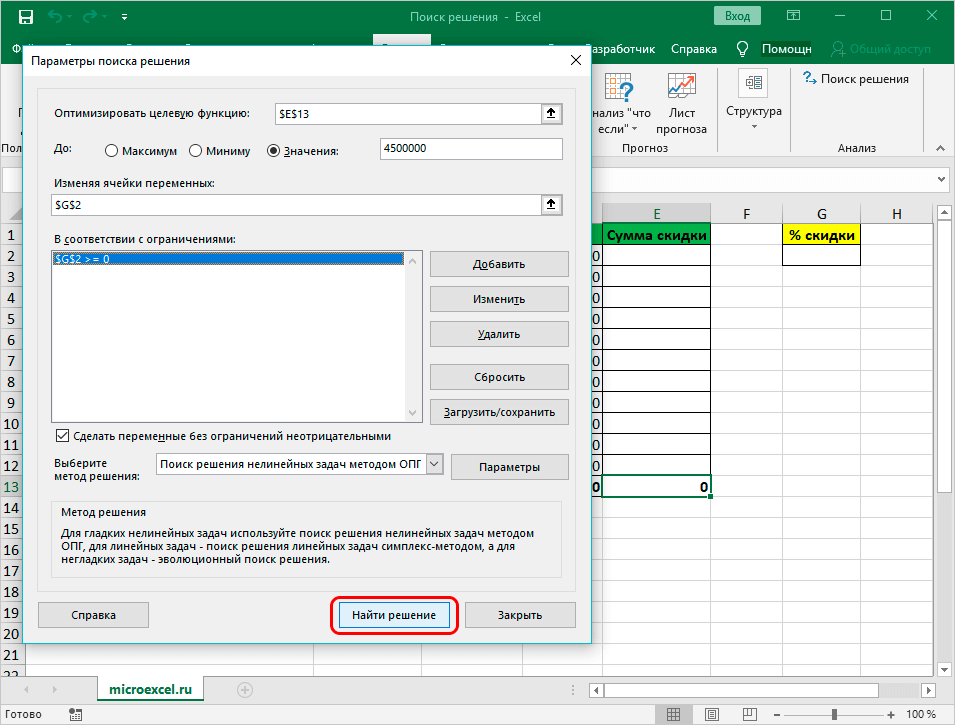
- После программа проводит требуемые расчеты и выдает конечные расчеты в необходимых ячейках. Потом открывается окно с результатами, где сохраняются/отменяются итоги либо настраиваются параметры поиска по новой. Когда данные соответствуют требованиям, то найденное решение сохраняется. Если заранее установить отметку «Вернуться в диалоговое окно параметров поиска решения», будет открыто окно с настройками функции.
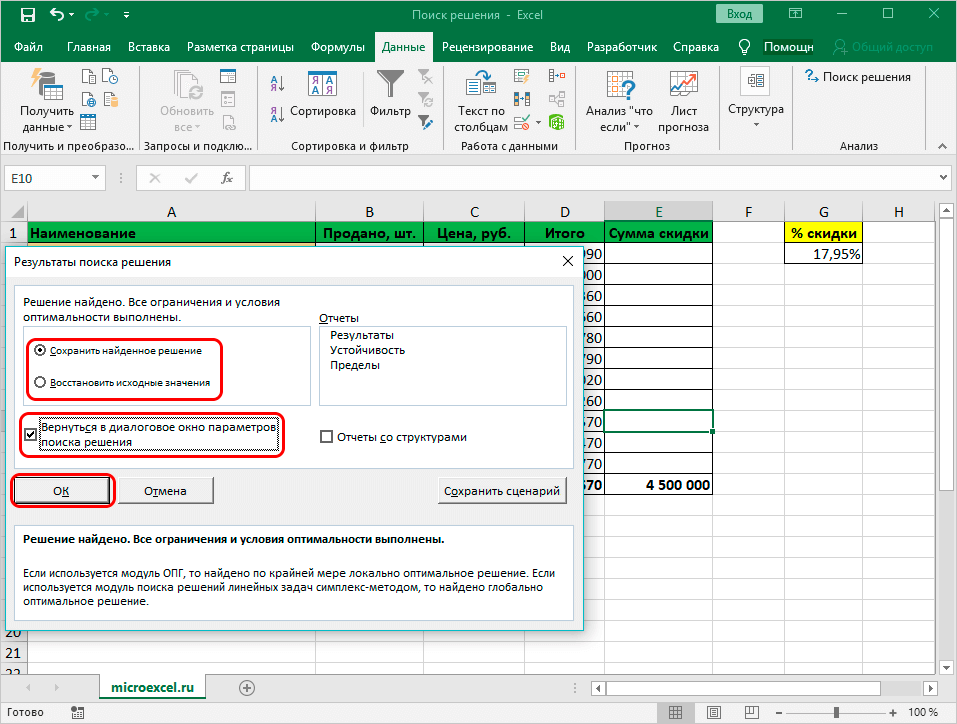
- Есть вероятность, что расчеты оказались ошибочными или есть необходимость в изменении исходных данных в целях получения других показателей. В такой ситуации требуется вновь открыть окно с настройками и перепроверить сведения.
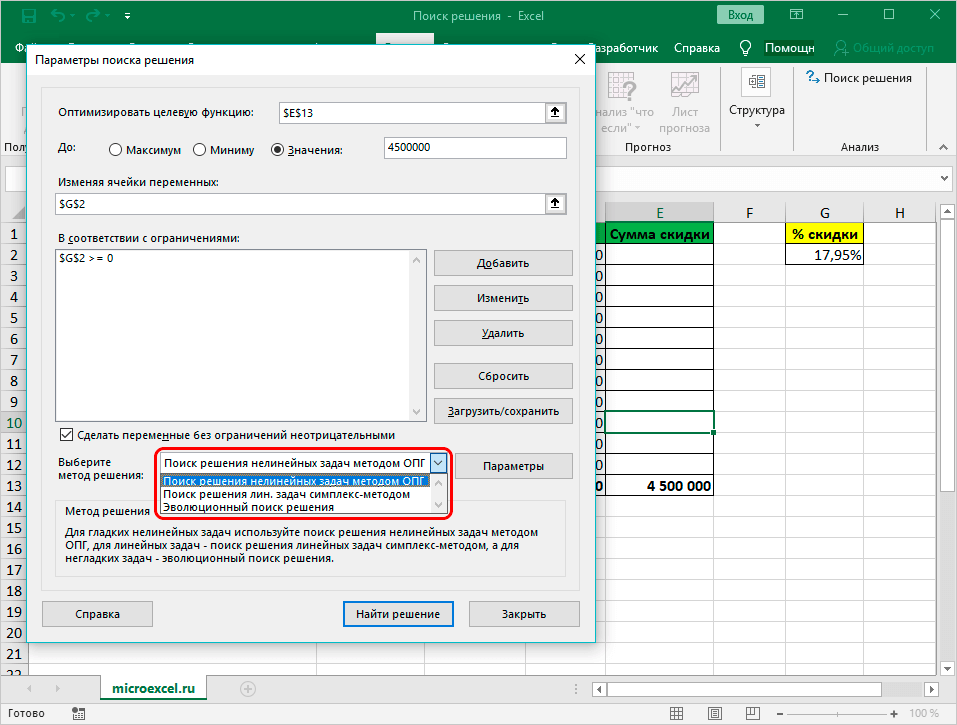
- Когда данные точны, можно воспользоваться альтернативным методом. В этих целях нужно нажать на текущий вариант и из появившегося списка выбрать самый подходящий способ:
- Поиск решения посредством обобщенного градиента для нелинейных задач. По умолчанию применяется такой вариант, однако возможно воспользоваться и другими.
- Поиск решения для линейных задач на основе симплекс-метода.
- Использование эволюционного поиска в целях выполнения задачи.
Внимание! Когда вышеназванные варианты не смогли справиться с задачей, следует осуществить проверку данных в настройках снова, так как это зачастую бывает основной ошибкой в таких задачах.
- Когда получена искомая скидка, остается ее применить для подсчета суммы скидок по каждому наименованию. В этих целях выделяется начальный элемент столбика «Сумма скидки», прописывается формула «=D2*$G$2» и жмется «Enter». Значки доллара проставляются, чтобы во время растягивания формулы на смежные строчки G2 не изменялась.
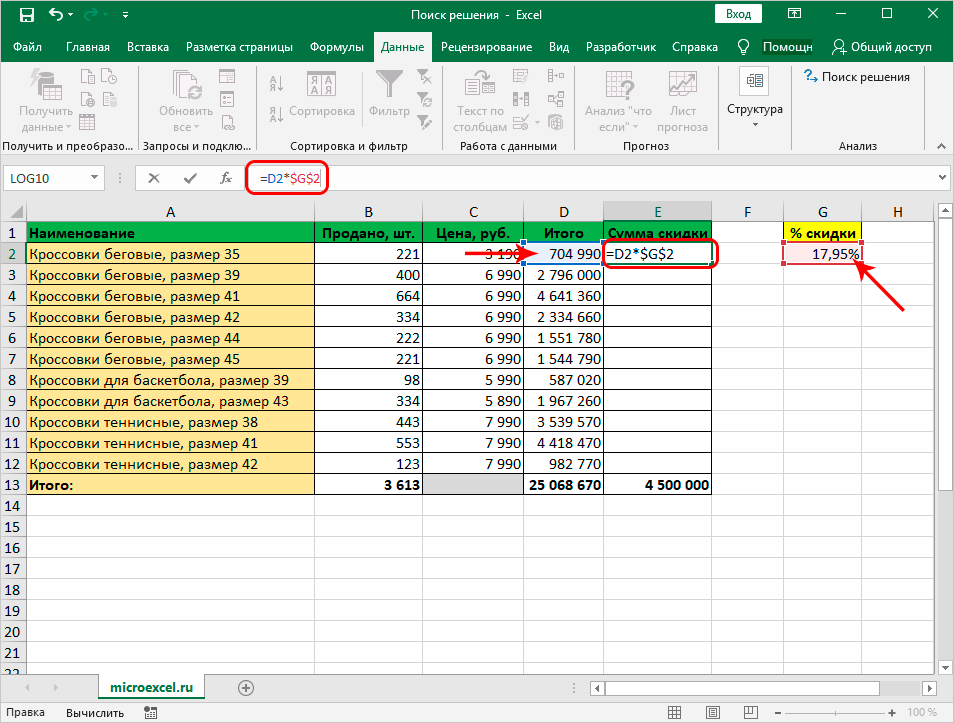
- Теперь будет получена сумма скидки для начального наименования. Затем следует навести курсор на угол ячейки, когда он станет «плюсом», зажимается ЛКМ и формула растягивается на необходимые строки.
- После этого таблица будет окончательно готова.
Загрузить/сохранить параметры Поиска решений
Данная опция полезна при применении различных вариантов ограничений.
- В меню «Параметры поиска решения» следует нажать «Загрузить/сохранить».
- Вводится диапазон для области модели и нажимается «Сохранить или Загрузить».
Во время сохранения модели вводится ссылка на 1 ячейку пустого столбца, где будет размещена модель оптимизации. В процессе загрузки модели вводится ссылка на весь диапазон, где содержится модель оптимизации.
Важно! Для сохранения последних настроек в меню «Параметры поиска решения» сохраняется книга. Каждый лист в ней имеет собственные параметры надстройки «Поиск решения». Помимо того, для листа возможно выставить больше 1 задачи при нажатии кнопки «Загрузить или сохранить» в целях сохранения отдельных задач.
Простой пример использования Поиска решения
Нужно провести загрузку контейнера тарой, чтобы его масса была максимальной. Емкость обладает объемом в 32 куб. м. Наполненная коробка имеет вес в 20 кг, ее объем равен 0,15 куб. м. Ящик – 80 кг и 0,5 куб. м. Требуется, чтобы общее число тары составляло не менее 110 шт. Данные организовываются так:
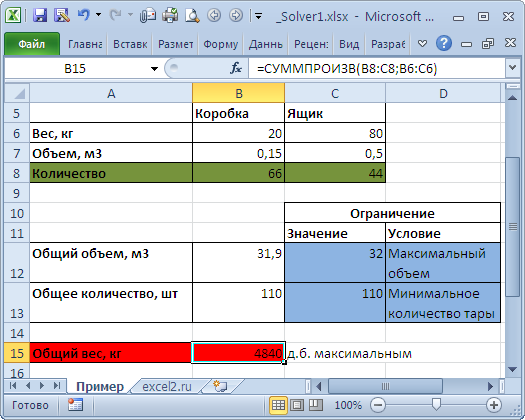
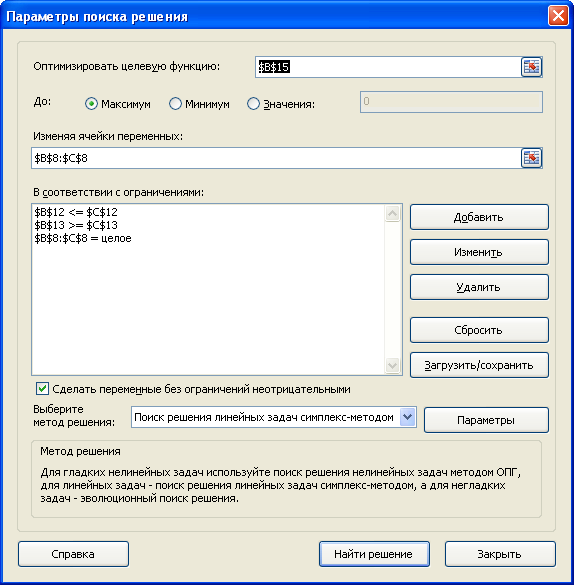
Переменные модели отметим зеленым. Целевая функция выделяется красным. Ограничения: по наименьшему количеству тары (больше либо равно 110) и по массе (=СУММПРОИЗВ(B8:C8;B6:C6) – суммарный вес тары, находящейся в контейнере.
По аналогии считаем общий объем: =СУММПРОИЗВ(B7:C7;B8:C8). Такая формула необходима, чтобы выставить ограничение на суммарный объем тары. Потом посредством «Поиск решения» вводятся ссылки на элементы с переменными, формулами и самими показателями (либо ссылки на конкретные ячейки). Разумеется, что количество тары – целое число (также является ограничением). Нажимаем «Найти решение», в результате чего находится такое число тары, когда общая масса максимальна и учтены все ограничения.
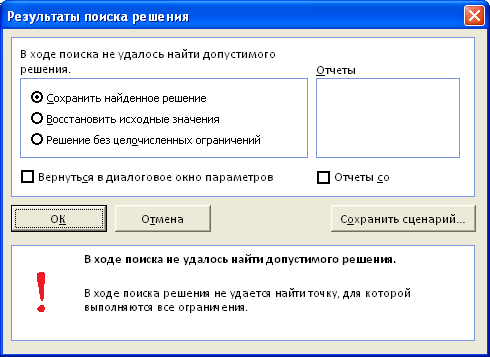
Поиску решения не удалось найти решения
Такое уведомление выскакивает, когда рассматриваемая функция не нашла сочетаний показателей переменных, удовлетворяющих каждому ограничению. При использовании Симплекс-метода вполне возможно, что решения нет.
Когда используется способ решения нелинейных задач, во всех случаях начинающийся с начальных показателей переменных, это свидетельствует о том, что возможное решение далеко от таких параметров. Если запустить функцию с прочими начальными показателями переменных, то, вероятно, решение найдется.
К примеру, во время использования нелинейного способа, элементы таблицы с переменными не заполнялись, и функция не нашла решений. Это не значит, что решения нет. Теперь, с учетом результатов определенной оценки, в элементы с переменными вводятся другие данные, близкие к получаемым.
В любой ситуации изначально следует изучить модель на отсутствие противоречия ограничений. Зачастую подобное взаимосвязано с ненадлежащим подбором соотношения либо предельного показателя.
В вышеуказанном примере показатель максимального объема указан 16 куб. м вместо 32, потому такое ограничение противоречит показателям по минимальным количествам мест, поскольку ему будет соответствовать число 16,5 куб. м.
Заключение
Исходя из этого, опция «Поиск решения» в Excel поможет в разрешении конкретных задач, которые довольно трудно либо невозможно решить обычными способами. Сложность в применении такого метода состоит в том, что изначально эта опция скрыта, ввиду чего большинство пользователей не знают о ее наличии. Кроме того, функция достаточно сложна в изучении и использовании, однако при надлежащем исследовании, она принесет большую пользу и облегчит расчеты.