Табличный процессор Эксель способен реализовывать большое число математических операций. Из статьи вы узнаете, как используется метод наименьших квадратов, который применяется для осуществления решения разнообразных задач.
Первоначальные настройки: включение параметра «Поиск решения»
Изначально необходимо включить «Поиск решения», так как по умолчанию он находится в выключенном состоянии. Пошаговое руководство выглядит следующим образом:
- Переходим в раздел «Файл», который находится в левом верхнем углу интерфейса табличного процессора.
- На экране отобразилось новое окошко. Здесь, в левой колонке, необходимо кликнуть на элемент «Параметры».
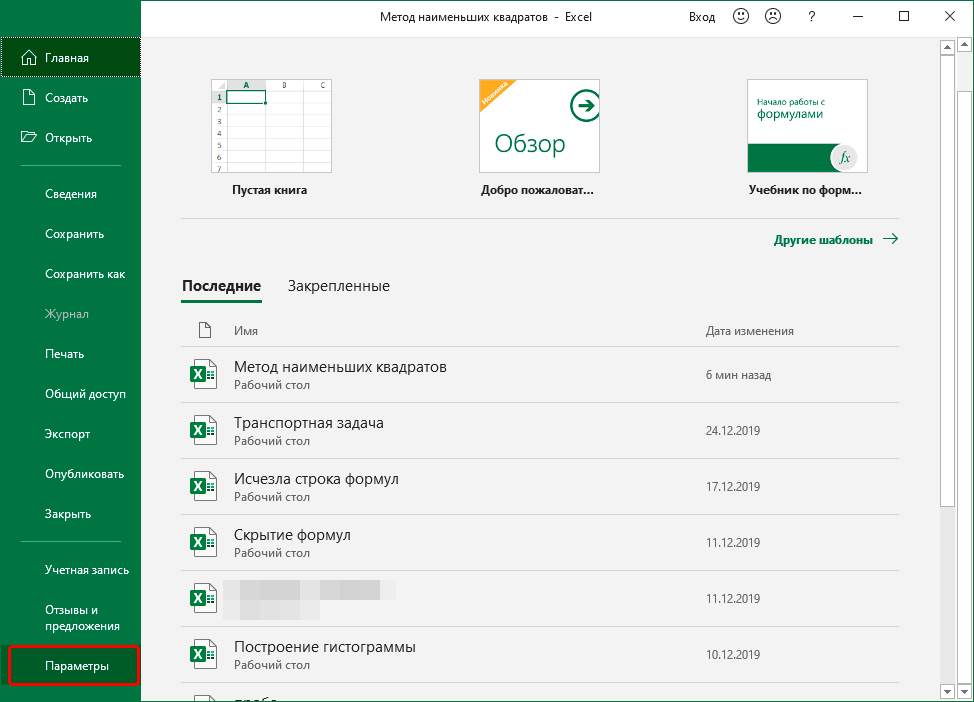
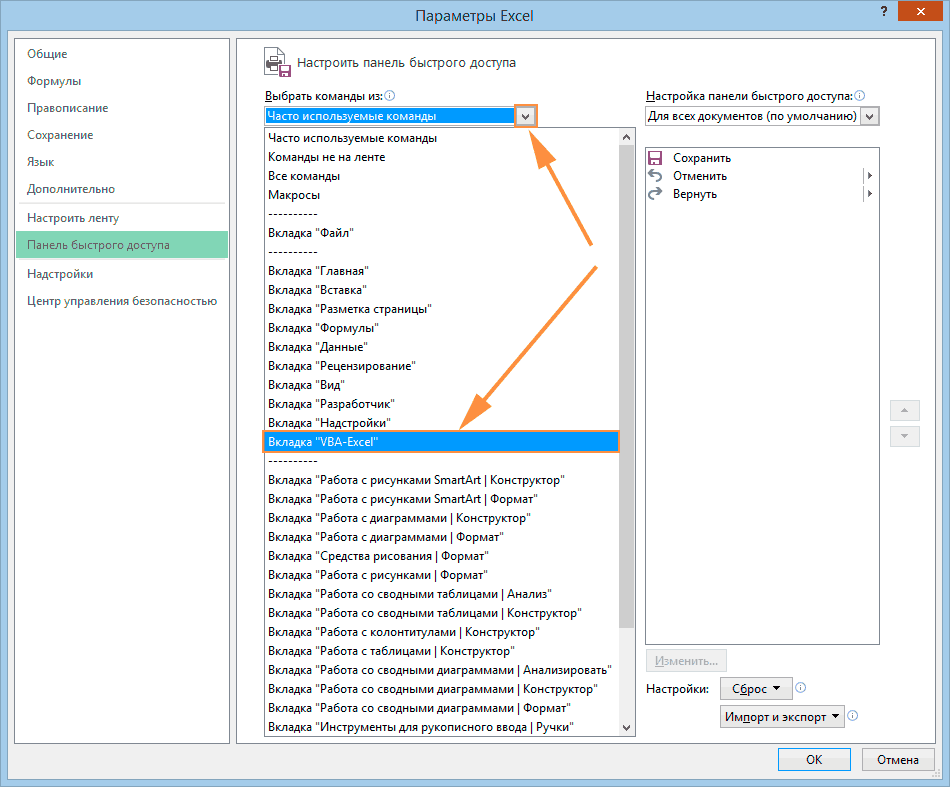
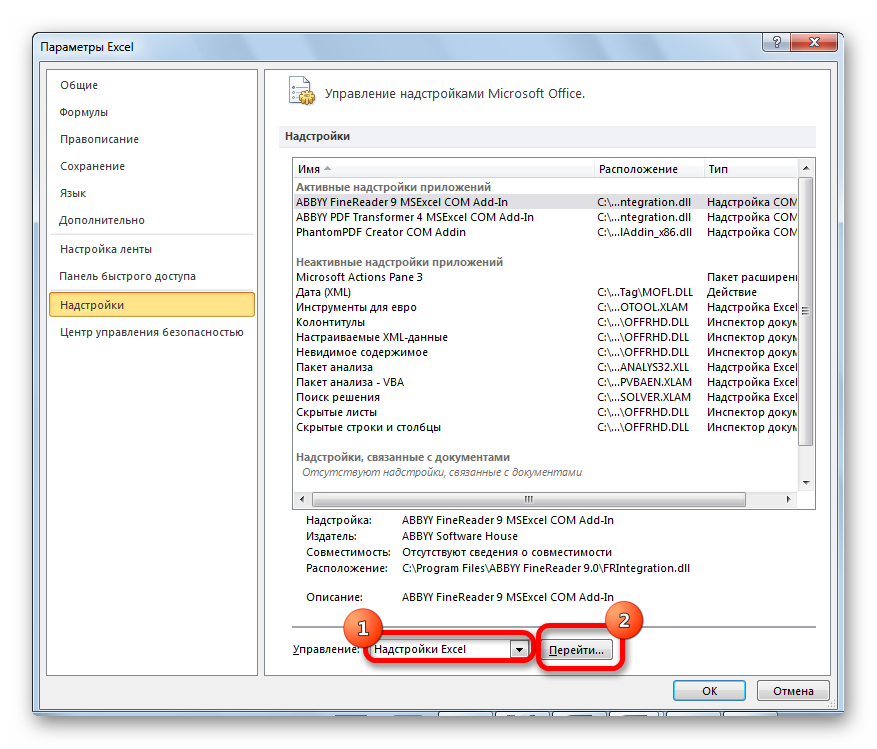
- В появившемся окне выбираем раздел «Надстройки». В правой части окошка находим надпись «Управление:» и раскрываем список. В списке выбираем пункт «Надстройки Excel». Щёлкаем кнопку «ОК».
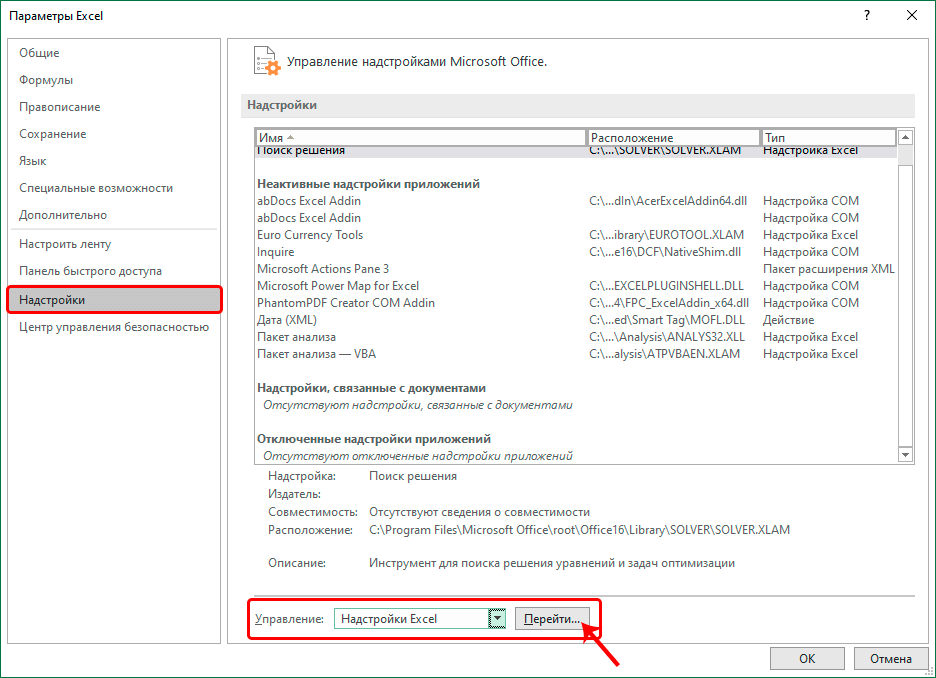
- Появилось еще одно окошко с названием «Надстройки». Около элемента «Поиск решения» ставим галочку. После проведения всех манипуляций кликаем «ОК».
- Готово! Параметр включился, и теперь мы можем приступить к разбору метода наименьших квадратов.
Что такое метод наименьших квадратов
Для начала вспомним, что метод наименьших квадратов — математический метод, используемый для решения задач, основанный на минимизации суммы квадратов отклонений некоторых функций от изначальных значений.
Он может применяться для «решения» переопределенных систем уравнений (когда число уравнений больше числа неизвестных), для поиска решения в случае стандартных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функции.
Шаг первый: исходные данные решаемой задачи
На конкретном примере начнем разбор метода наименьших квадратов. К примеру, у нас есть 2 колонки – X и Y:
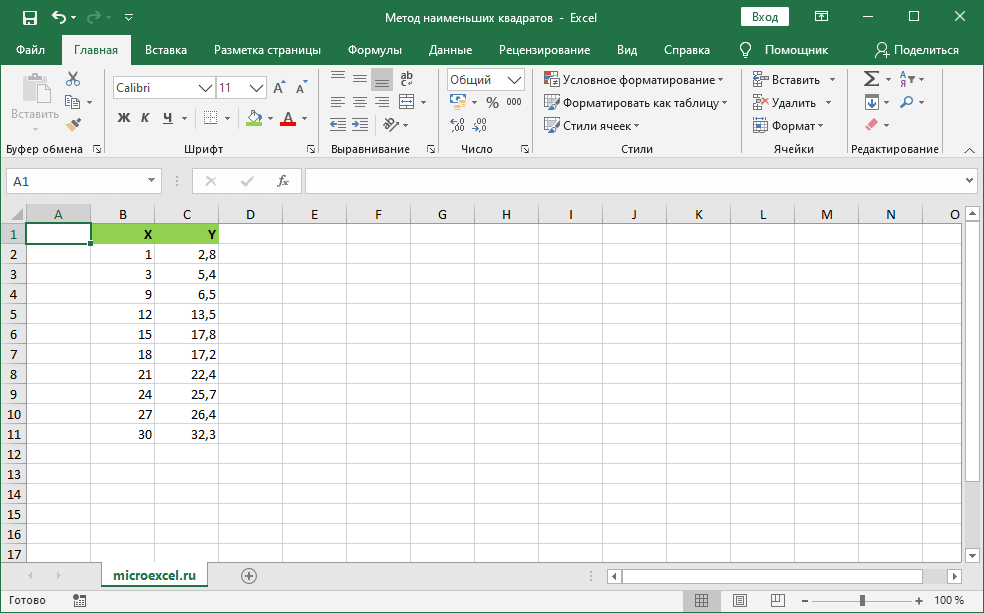
Эта зависимость описывается уравнением: Y=A+NX.
Мы прекрасно знаем, что если Х равен нулю, то и Y равен нулю. Следовательно, это уравнение можно привести к следующему виду: Y=NX. Начнём реализацию этой задачи. Нам нужно найти сумму квадратов разности.
Шаг второй: решение задачки с использованием МНК
Пошаговое руководство выглядит следующим образом:
- Столбику, который располагается левее показателя Х, даем название N и прописываем единицу рядом с 1-м показателем колонки Х. Единица – это примерное значение 1-го коэффициента N.
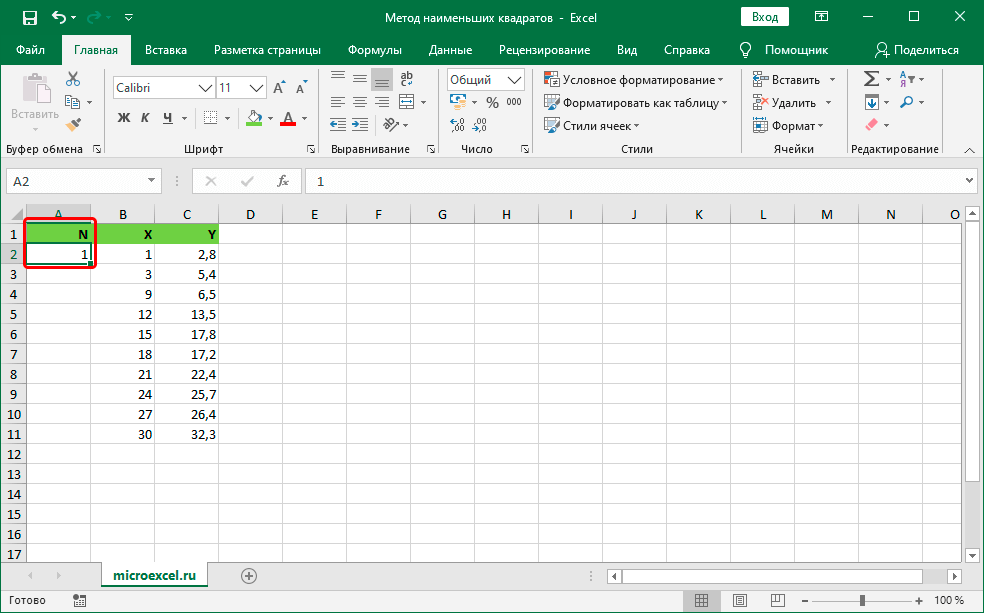
- Столбику, который располагается правее показателя Y, даем наименование NX.
- В ячейку D1, находящуюся около первых показателей X и Y, прописываем специальную формулу произведения коэффициента N на показатель из столбика Х. Сама формула выглядит следующим образом: =$А$2*В2. Стоит заметить, что адрес ячейки с коэффициентом необходимо привести к абсолютному типу. Абсолютный тип в табличном процессоре позволяет зафиксировать строчку или столбик (или все вместе одновременно). Иными словами, при копировании значений в другие ячейки абсолютные ссылки не будут меняться. После проведения всех манипуляций жмем клавишу «Enter».
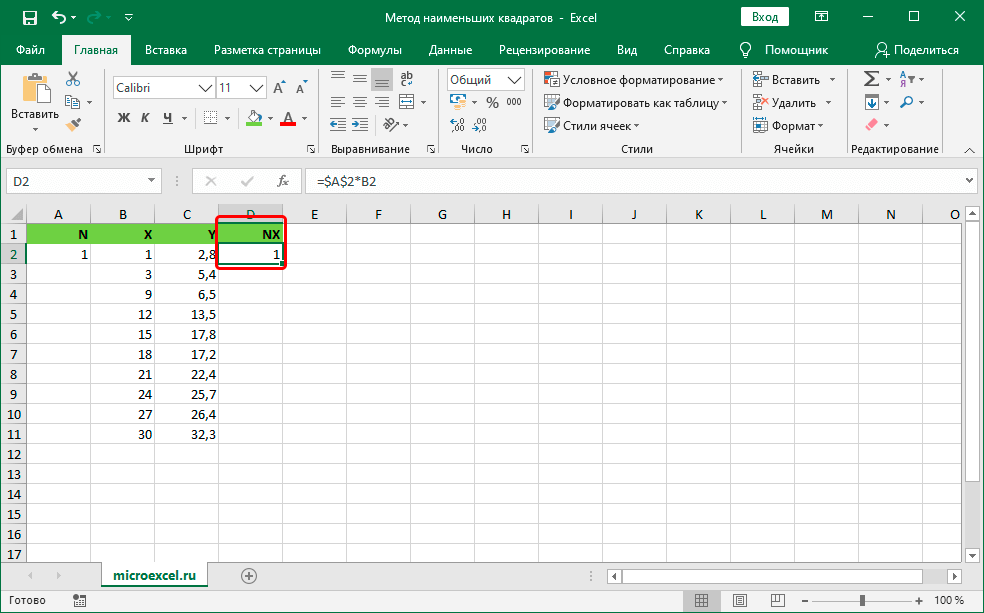
- Перемещаем курсор мышки на сектор с выведенным результатом. Наведя указатель в правый верхний уголок, он превратится в маленький плюсик темного цвета, который называется маркером заполнения. Зажимаем ЛКМ и перетягиваем маркер в самый низ до крайней строчки табличных данных.
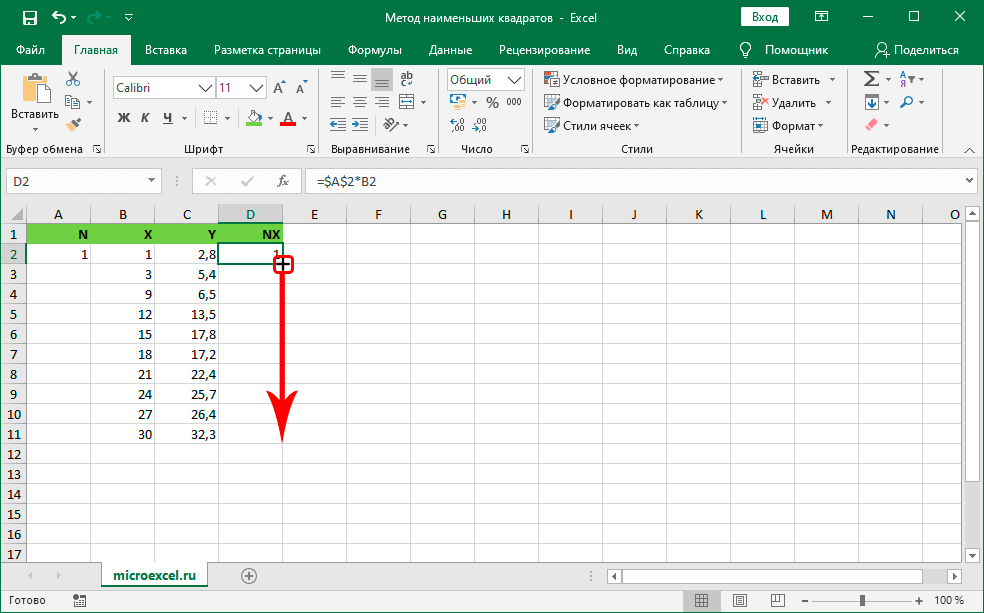
- После проведения этих манипуляций мы получили результаты вычислений во всех секторах колонки NX.
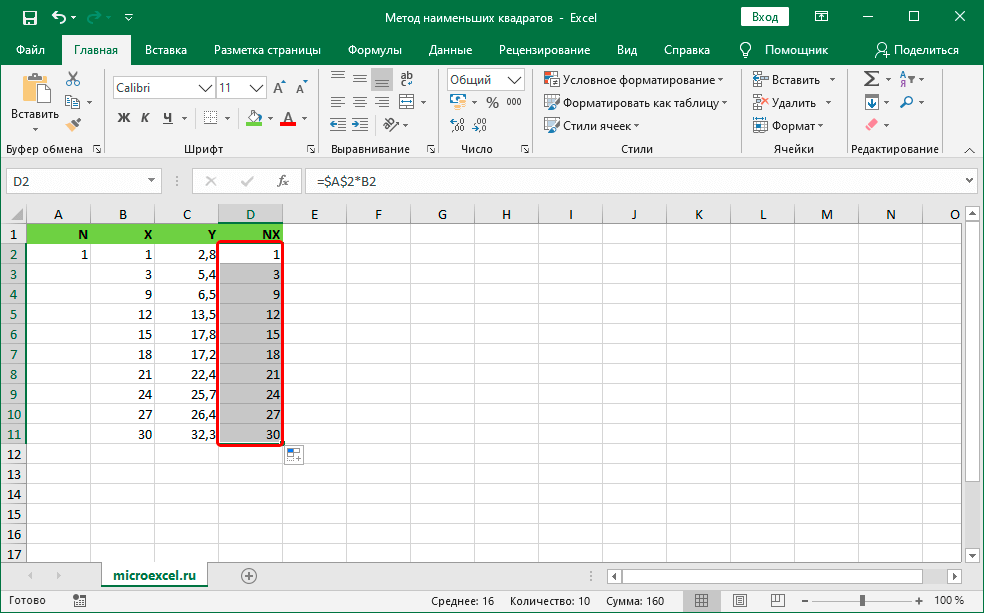
- Далее переходим к подсчету суммы разностей квадратов показателей Y и NX. Перемещаемся в ячейку E1, располагающуюся правее от показателя NX, нажимаем на элемент «Вставить функцию», который находится рядом со строкой для ввода формул, и имеет внешний вид «fx».
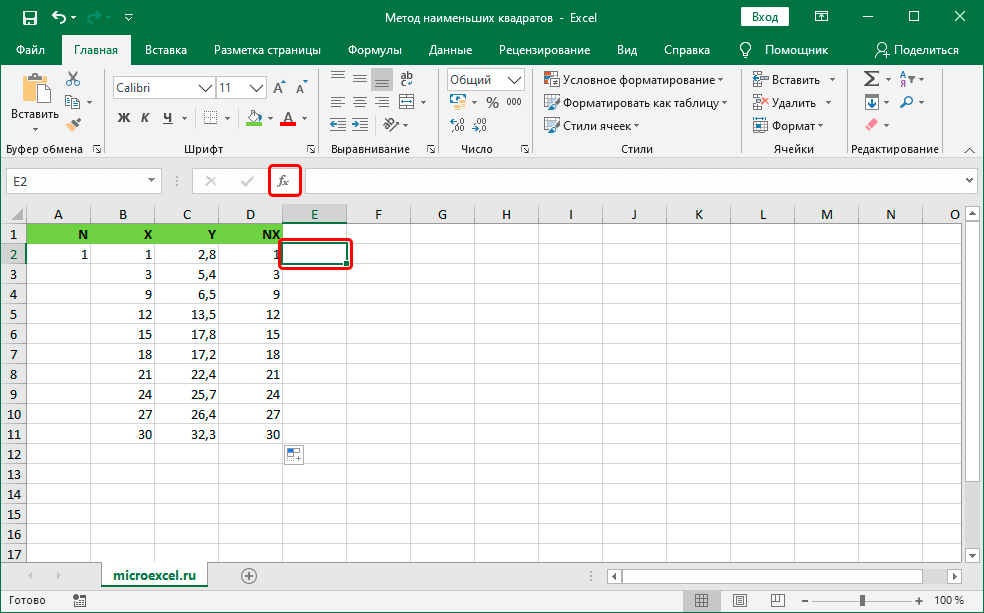
- Первым делом, находим надпись «Категории:» и раскрываем список, находящийся рядом. В обширном списке выбираем элемент «Математические». В блоке «Выберите функцию:» отыскиваем функцию «СУММКВРАЗН» и выбираем ее. После проведения всех манипуляций жмем на кнопку «ОК».
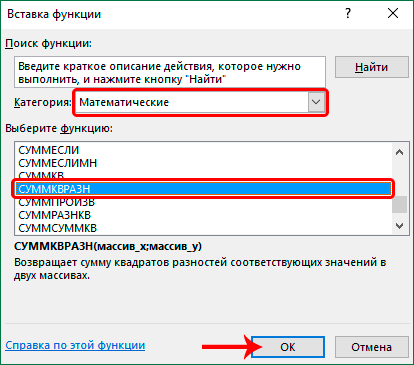
- Открылось небольшое окошко «Аргументы функции». Для дальнейшей работы необходимо заполнить все строки формы. В строчку «Массив_х» вводим адрес диапазона ячеек столбика Y. Координаты можно вписать самостоятельно ручным вводом, используя клавиатуру, или же путем их выбора в самих табличных данных.
- В строчку «Массив_у» вводим адрес диапазона ячеек столбика NX. После проведения всех манипуляций щёлкаем клавишу «Enter».
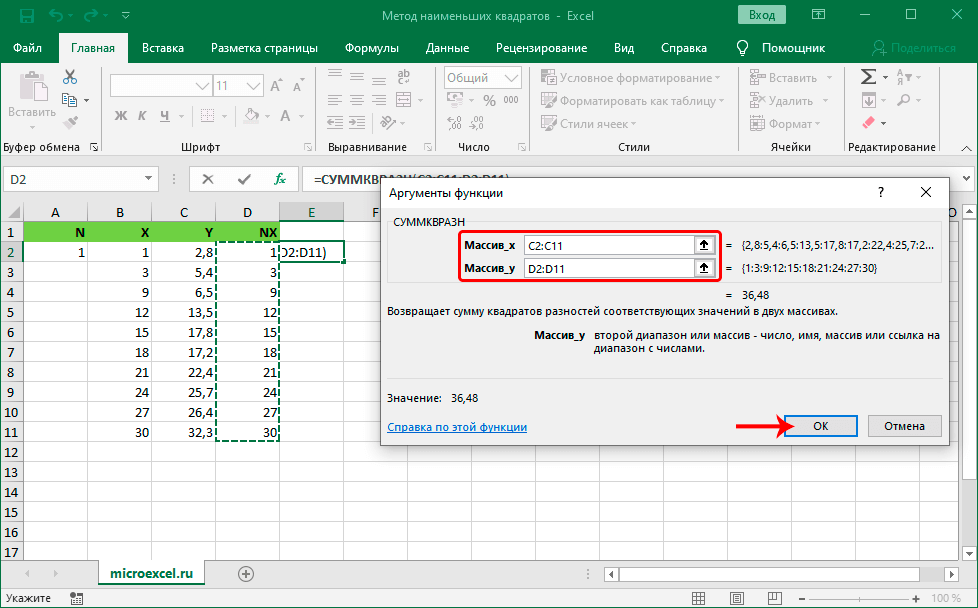
- Перемещаемся в раздел «Данные», который находится в верхней части интерфейса табличного процессора. Находим блок команд под названием «Анализ» и выбираем элемент «Поиск решения».
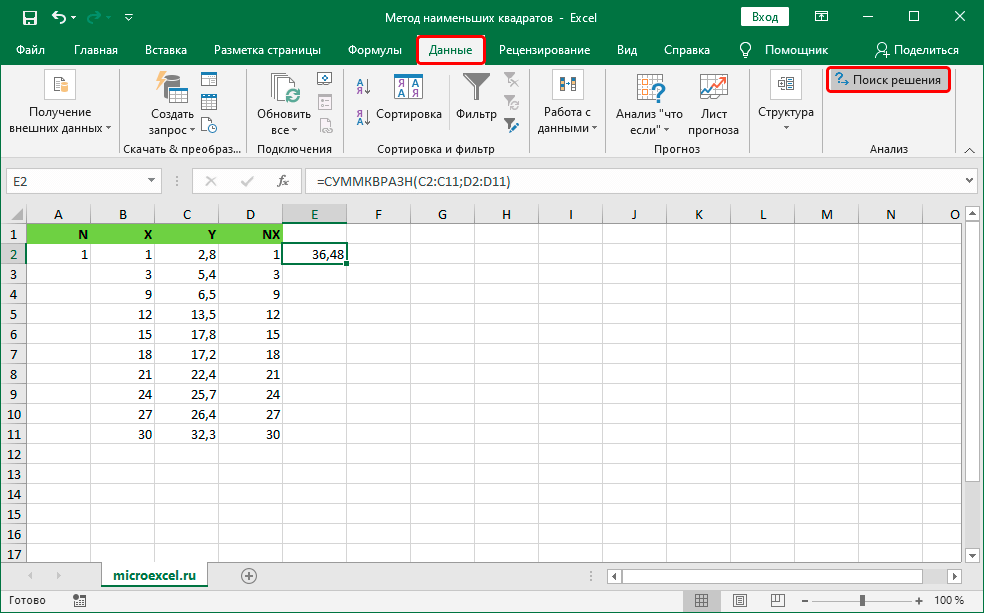
- На экране отобразилось окошко с огромным количеством настроек, которые необходимо заполнить. В строчку «Оптимизировать целевую функцию» вводим ссылку на ячейку с оператором «СУММКВРАЗН». Реализовать это действие можно самостоятельно ручным вводом, используя клавиатуру, или же выбрав сектор в самой табличке. Ставим отметку около надписи «Минимум», которая располагается в блоке «До:». В строчку «Изменяя ячейки переменных» вбиваем адрес сектора, в котором располагается показатель коэффициента N – $A$2. После проведения всех манипуляций щелкаем на «Найти решение».
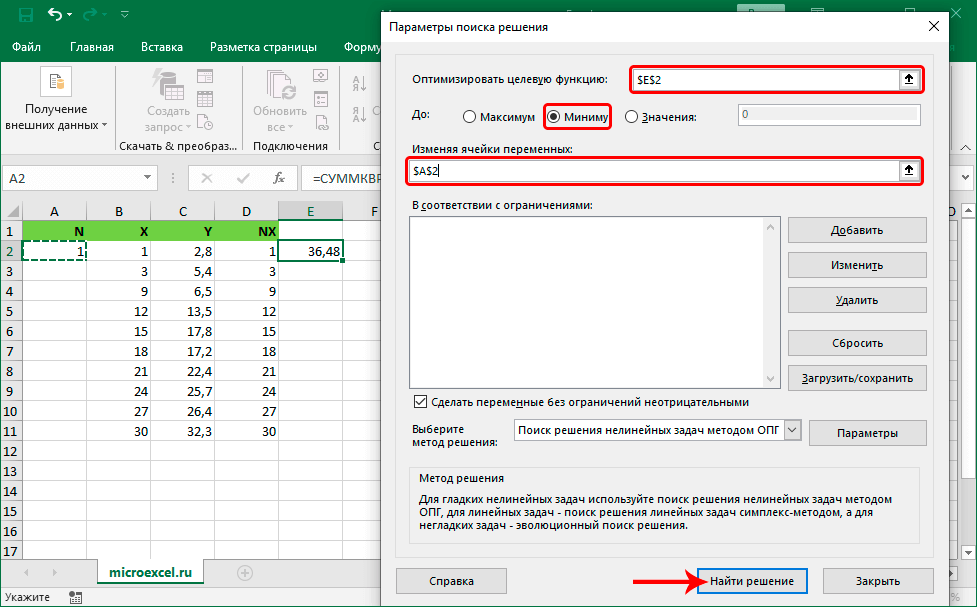
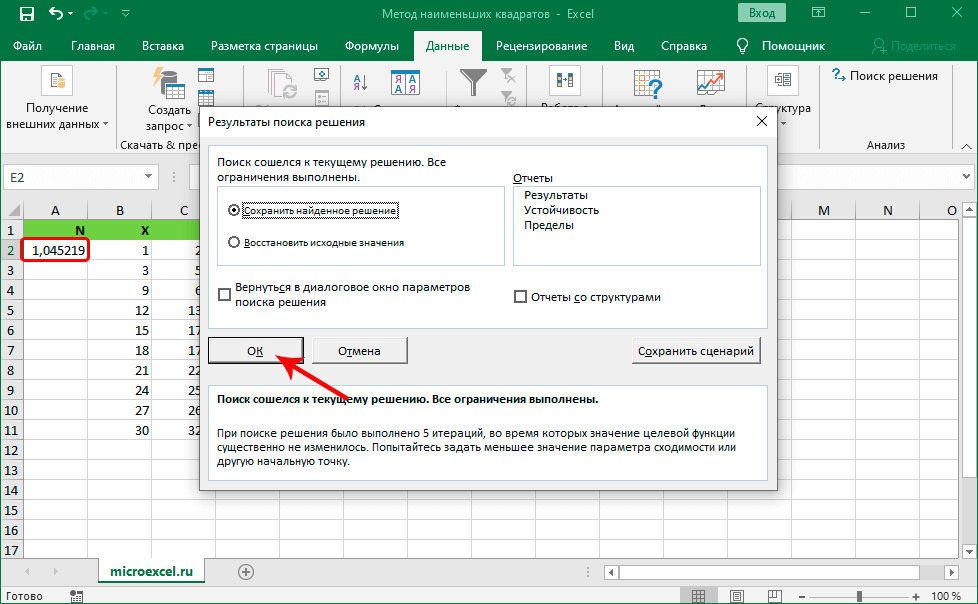
- После того, как «Поиск решения» будет выполнен, на экране компьютера отобразится окошко с выведенными результатами поиска решения, а затем реализуется замена числовых значений в столбике N. Отображенный результат – это наименьший квадрат функции. Если выведенный результат удовлетворяет тому, что нужно было найти, то нажимаем «ОК».
Заключение
Таким образом, мы на конкретном примере рассмотрели способ использования метода наименьших квадратов в табличном процессоре Microsoft Excel и ознакомились со стандартным алгоритмом действий при решении похожих задач.