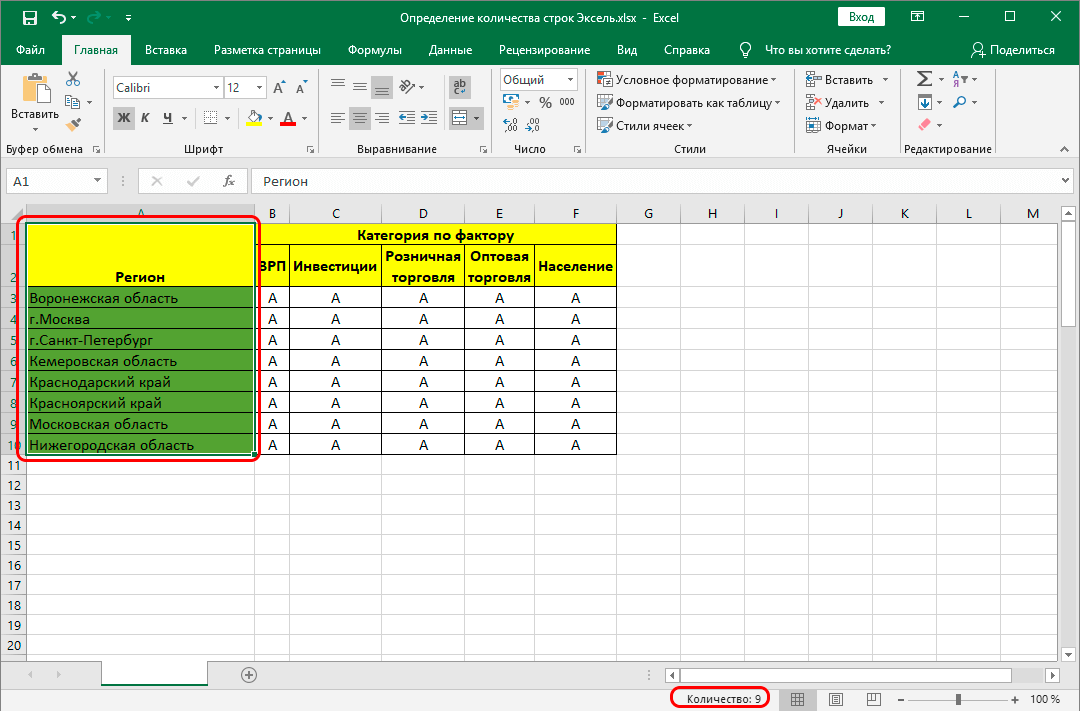
Статистика – наука, которая используется для любых других исследований, а также обработки большого количества количественных и даже качественных данных. И что важно, это одно из главных применений электронных таблиц Excel, поэтому давайте более подробно рассмотрим, статистические формулы. Во-первых, что они нам дают? Прежде всего, они позволяют структурировать информацию и осуществить ее анализ. Статистические функции в Excel относятся к совершенно отдельной категории.
Как пользоваться статистическими функциями
Есть несколько способов ввода любой функции, и статистические не являются исключением:
- Ввести непосредственно в ячейке, предварительно нажав клавишу =. Это касается самых простых функций, несложных для запоминания и содержащих один или два аргумента. Например, так можно делать для операции умножения, сложения, вычитания и деления. А вот если функция сложная, то можно воспользоваться помощником. Это уже второй способ.
- Помощник по использованию функций. Он не только подсказывает, какая формула что означает, а и помогает ввести правильные аргументы применительно к конкретной функции.
Вызвать помощник можно несколькими способами:
- Воспользоваться кнопкой «Вставить функцию», расположенной слева от строки формул.
- Вызвать мастер ввода функций через кнопку «Вставить функцию», которая находится в левой части панели, которая открывается по клику на вкладку «Формулы».
- Воспользовавшись горячими клавишами Shift+F3.
Любой из этих методов приводит к одному результату – вызову мастера функций. Можно использовать тот, который больше всего подходит в конкретной ситуации. После того, как окно откроется, нам первым делом нужно выбрать категорию: статистические функции. 
После того, как тип функции будет выбран, нам нужно выбрать подходящую формулу из списка. Под перечнем видим, что есть описание, в котором рассказывается, что конкретная функция делает. 
Чтобы подтвердить выбор функции, которая будет вводиться, нужно нажать клавишу ОК. После этого появится такое окно, в котором можно ввести параметры функции (или, как их еще называют, аргументы). 
Интересный факт. Можно выбрать функцию еще одним способом. Для этого нужно перейти на вкладку «Формулы» и нажать на кнопку «Другие функции», расположенной на ленте.
Далее будет пункт «Другие функции» – «Статистические» и в появившемся списке ищем подходящую функцию и выбираем ее. Этот перечень может прокручиваться. 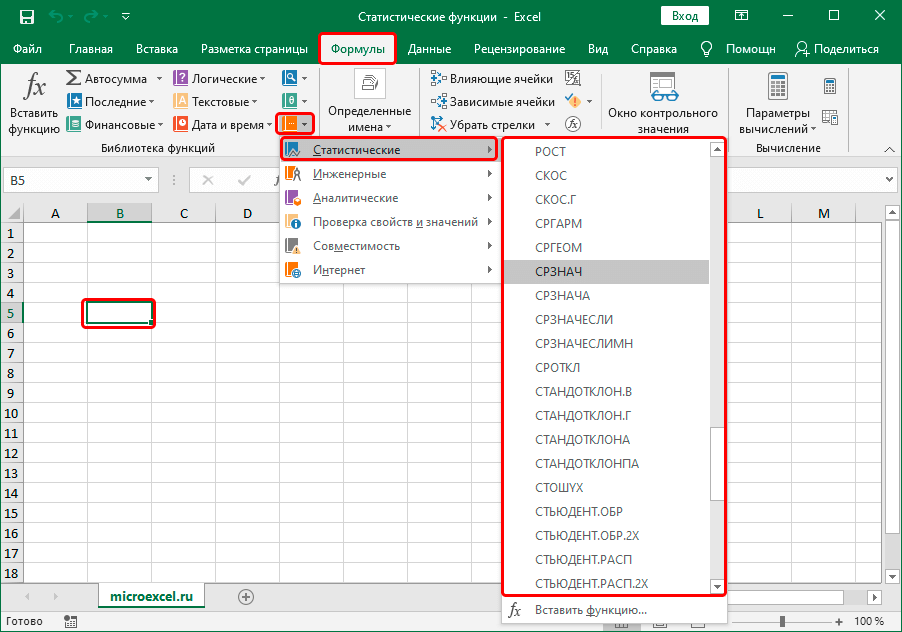
Перечень статистических функций
А теперь давайте перейдем непосредственно к рассмотрению статистических функций.
Функция СРГЕОМ
Много кто знает о таком параметре, как среднее арифметическое. Вычисляется оно с помощью функции, о которой мы еще сегодня обязательно поговорим. Но есть еще одна функция, которая определяет среднее геометрическое. 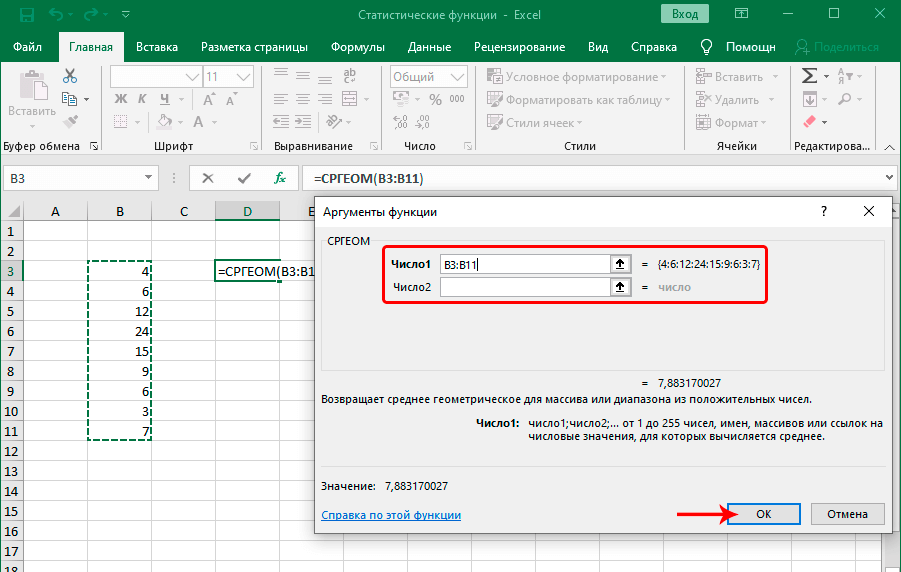
Формула очень простая: =СРГЕОМ(число1;число2;…). Кроме чисел также можно указать диапазон значений, которые учитываются этой функцией. Что же такое среднее геометрическое? Это число, которое может заменять любое из чисел в последовательности таким образом, чтобы не менялось произведение этих значений. Еще один часто используемый термин – среднее пропорциональное. Это синоним к среднему геометрическому. Такой второй термин используется, потому что среднее геометрическое пропорционально к первому и второму числам.
Функция СТАНДОТКЛОН
Один из главных статистических параметров, который должен рассчитываться вместо со средним арифметическим – стандартное отклонение. Это мера, демонстрирующая степень разброса значений. Выполняет ту же функцию, что и дисперсия, просто представлена в том же виде, что и среднее значение, в отличие от дисперсии.
Вообще, стандартное отклонение рассчитывается, как квадратный корень из дисперсии. Но в Эксель есть специальная формула, которая сразу вычисляет степень дисперсии, после чего на основе полученного значения получает стандартное (или среднеквадратическое) отклонение.
Сама эта формула довольно старая, но знать о ней надо, потому что время от времени ее можно найти в готовых таблицах. Сейчас уже есть более новые версии этой функции – СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г. Последняя функция находит среднеквадратическое отклонение по генеральной совокупности, в то время как первая ориентируется исключительно на выборку.
В остальном, синтаксис обеих функций такой же, как и для вычисления среднего арифметического (об этом мы поговорим позже) – числа, которые перечислены через скобку.
Функция МОДА.ОДН
Мода выборки абсолютно не связана с одеждой или популярными машинами. Но при этом она связана со словом «популярный». Если говорить о статистике, то это значение в выборке, которое встречается наиболее часто. Соответственно, функция МОДА.ОДН дает возможность определить это значение.
Если говорить о синтаксисе, то он похож на многие другие статистические функции. Сначала пишется оператор, после чего в скобках записываются его аргументы, которые являют собой числа, разделенные запятой. В качестве значения аргумента может выступать не только число, но и отдельные ячейки, диапазоны значений. Это дает возможность более гибко управлять выборкой. На этом скриншоте отчетливо видно, как это работает на практике.
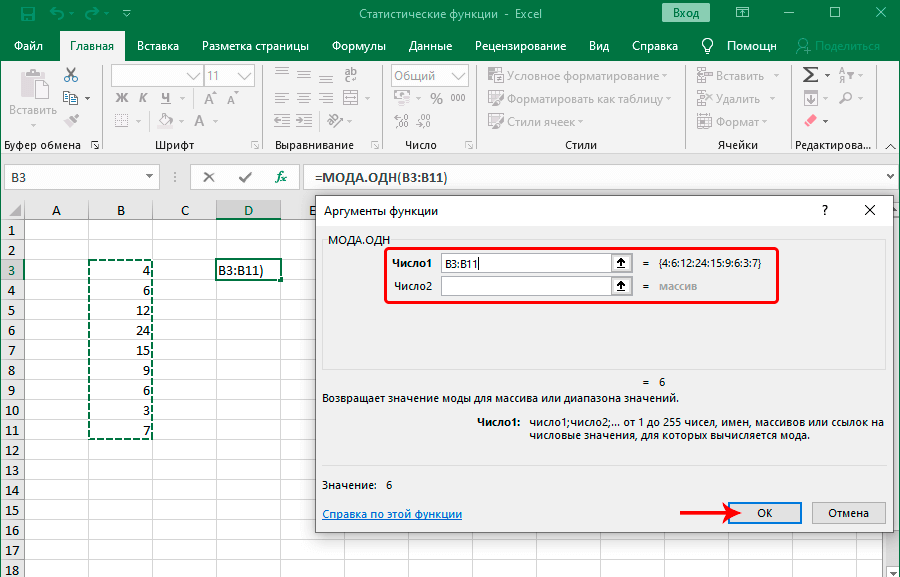
Эта функция подходит для горизонтальных массивов. Если же нужно определить моду выборки для вертикального массива, используется похожая функция МОДА.НСК. Общий внешний вид функции следующий: =МОДА.ОДН(аргумент 1, аргумент 2; аргумент …).
Функция НАИМЕНЬШИЙ
Задача этой функции – выполнение поиска из того набора значений, который был указан пользователем. Принцип ее работы такой же, как и следующий, только поиск осуществляется по направлению снизу вверх, от наименьшего числа к самому большому. Синтаксис этой функции предельно простой: =НАИМЕНЬШИЙ(массив;k).
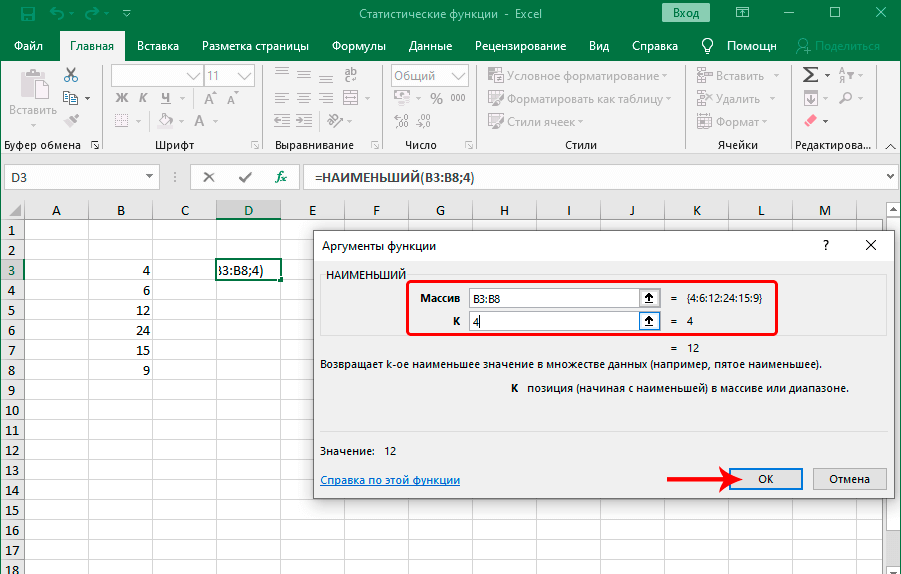
Функция имеет два основных аргумента: массив данных, по которым будет осуществляться поиск и порядковый номер элемента, который надо найти. Далее функция работает следующим образом: сначала она ищет самое маленькое значение, потом начинает перебирать цифры снизу вверх. Первое значение считается 1. То есть, если использовать число 1 во втором аргументе, то результат будет эквивалентным функции МИН, о которой мы поговорим немного позже.
Функция НАИБОЛЬШИЙ
Функция НАИБОЛЬШИЙ является аналогичной, только отсчет выполняет, начиная с самого большого значения. После того, как передать ей коэффициент, она ищет в порядковом ряду с большего в меньший число, занимающее соответствующее место и возвращает его. Работают обе функции аналогичным образом. Предположим, у нас есть числовой ряд. Если в нем в качестве числа k указать 2, то в результате получится число 15, поскольку оно является вторым по величине в диапазоне, который прописан в первом аргументе.
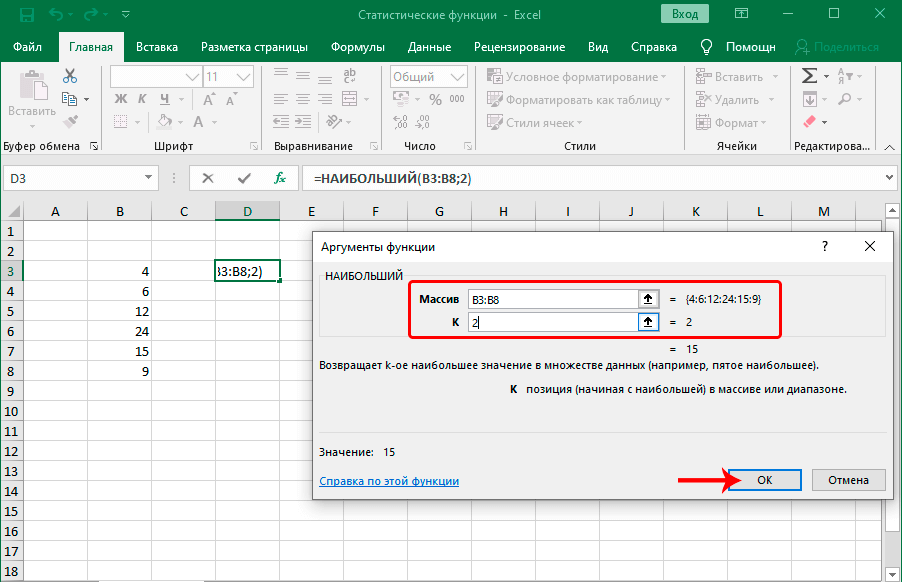
Эта функция может быть полезной в ситуациях, например, когда товар поступал в определенной последовательности, и нужно определить, сколько стоила, например, шубка, которая пришла второй по счету.
Функция МЕДИАНА
В статистике медиана – это разновидность среднего числа, которое находится ровно посередине числового ряда. Очень часто медиана является лучшим решением, чем стандартное среднее арифметическое, потому что позволяет определить действительно среднестатистическое значение. Синтаксис этой функции аналогичен тому, который имеет любой другой оператор, определяющий среднее значение – перечень цифр, ячеек или диапазонов, из которых данные будут получаться.
На этом примере видно, как на практике осуществляется работа с функцией. В диалоговом окне «Аргументы функции» можно вводить большое количество чисел, ячеек и диапазонов. На картинке мы попробовали ввести число в первую строку, ячейку во вторую и диапазон значений в третью. Получили в результате число 12. Максимальное количество аргументов этой функции – 255, что более, чем достаточно для полноценного использования этой функции. 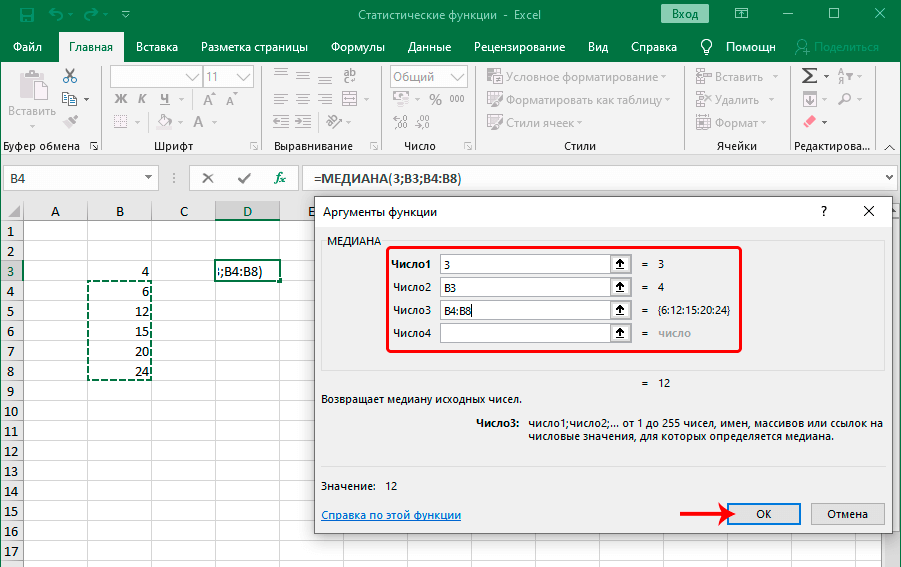
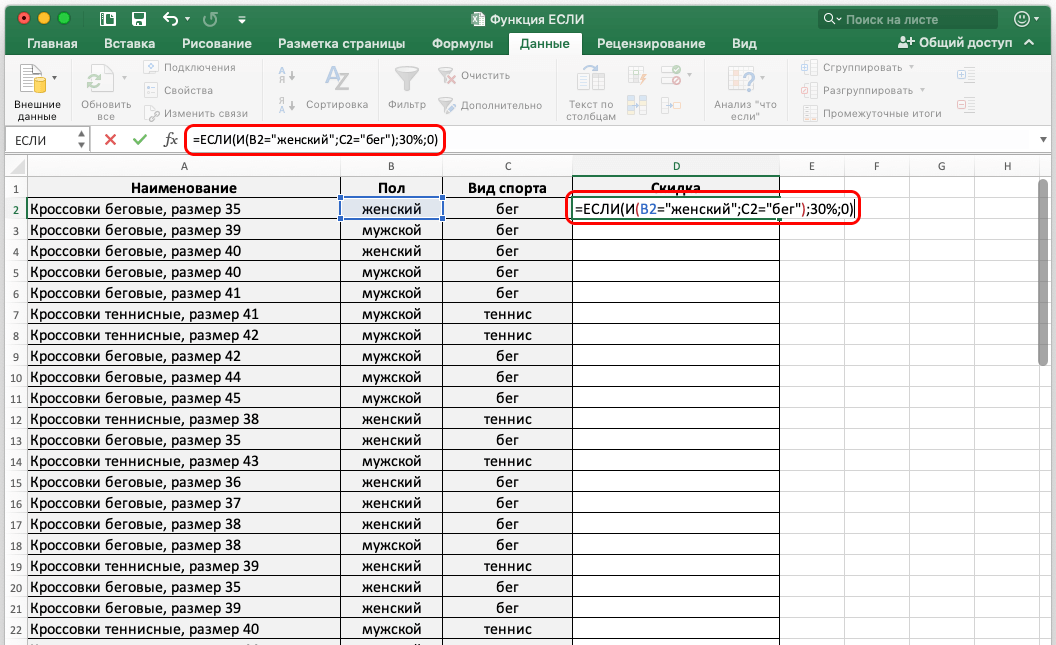
Функция СРЗНАЧЕСЛИ
Это улучшенная версия функции СРЗНАЧ, задача которой – находить среднее арифметическое, но лишь при условии, что определенное условие выполняется. Эта функция уже несколько сложнее тех, которые приводились выше: =СРЗНАЧЕСЛИ(диапазон;условие;диапазон_усреднения). Давайте рассмотрим каждый аргумент более подробно:
- Диапазон. Это ячейки, которые проверяются на предмет соответствия определенному условию.
- Условие. Это критерий, на предмет соответствия которому проверяется диапазон.
- Диапазон усреднения. Это тот диапазон, из которого будет доставаться среднее арифметическое. Этот аргумент вводить необязательно, поскольку диапазон ячеек и диапазон усреднения могут совпадать.
Функция МИН
В статистических подсчетах нередко нужно не только определить среднее значение, среднеквадратическое отклонение и вычислить другие показатели. Также важно значение наименьшего и наибольшего числа, в том числе, для получения указанных показателей. Практическое применение этой функции довольно обширное:
- На рынке акций для определения времени, когда цела была наиболее низкой.
- Для определения слабых мест в годовом бюджете (например, в каком месяце доходы компании были минимальными) с целью их дальнейшего исправления. Например, можно определить наименее доходный месяц и проанализировать факторы, которые этому способствовали.
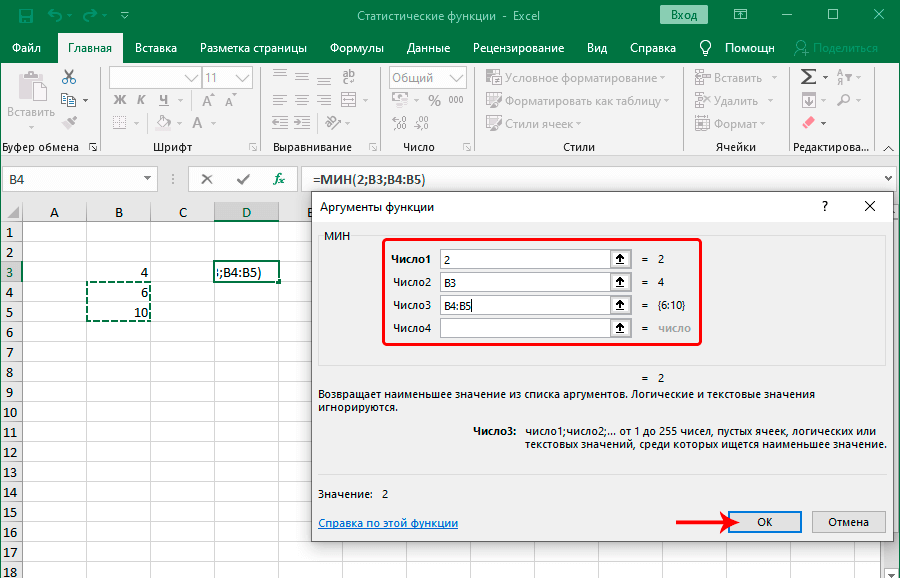
Существует огромное количество других ситуаций, когда можно использовать функцию МИН. В самом общем виде она выглядит следующим образом: =МИН(число1;число2;…). Принцип заполнения аргументов этой функции аналогичен функции МАКС.
Функция МАКС
Как становится понятно из названия, эта функция ищет максимальное значение в определенной числовой выборке. Ситуации, в которых она может использоваться, в принципе, те же за тем лишь исключением, что все в противоположную сторону. Например, компания может с помощью функции МАКС определить самый доходный месяц и понять, каковы причины этого успеха.
Функции СРЗНАЧ и СРЗНАЧА
Стандартная функция СРЗНАЧ определяет среднее арифметическое в числовой выборке. Общий вид формулы такой же, как и для любой другой выборки значений. Сначала пишется название функции, после чего в скобках приводятся числа и диапазоны, которые необходимо обработать с помощью этой функции. То есть, общий вид формулы следующий: =СРЗНАЧ(число1;число2;…).
Как мы поняли, можно использовать как обычные числа (очень полезно для использования значений, которые не будут меняться в течение ближайшего времени), ссылки на ячейку (они применяются для тех значений, которые в будущем изменятся) и на диапазон (в этом случае будет использоваться целый набор чисел за один раз). Чтобы после ввода одного аргумента начать записывать другой, достаточно нажать на соответствующее поле в мастере функций или просто нажать на клавишу Tab.
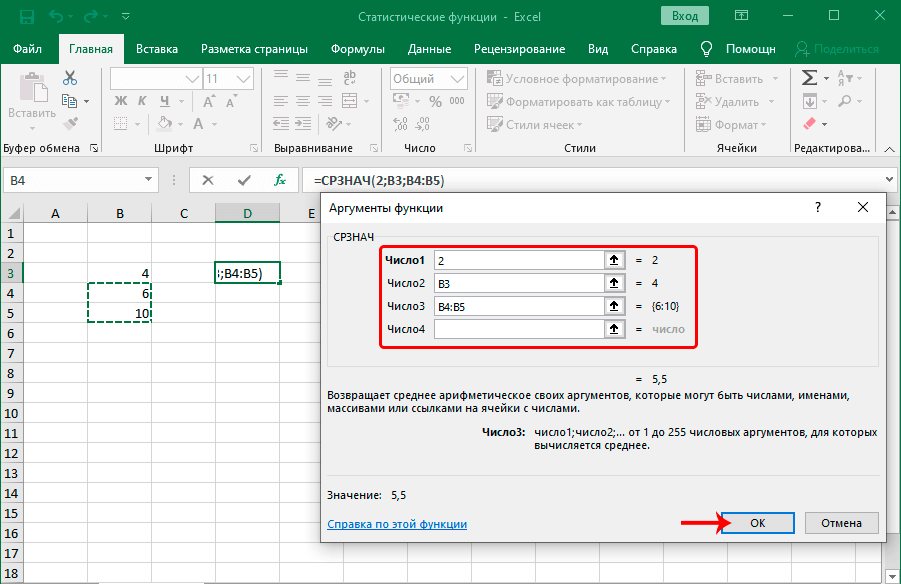
Максимальное количество аргументов, которые можно использовать в этой функции – 255. При этом обязательным аргументом является только первое число. В качестве аргументов не могут использоваться текстовые и логические значения. Они просто не учитываются формулой, в которой используется указанный оператор. Основное отличие функции СРЗНАЧА от СРЗНАЧ заключается в том, что текстовые значения и «ЛОЖЬ» считаются нулевыми, а значение «Истина» приравнивается к единице.
Функция РАНГ.СР
С помощью функции РАНГ.СР пользователь может вернуть ранг числа. Если несколько чисел в одном диапазоне относятся к одному рангу, то возвращается среднее. Имеет три аргумента, два из которых – обязательные:
- Число. Это то число, для которого осуществляется определение ранга.
- Ссылка. Это массив чисел, или ссылка на этот массив.
- Порядок. Это число, которое влияет на способ, в который значения будут упорядочиваться.
Таким образом, статистические функции Excel – это превосходный инструмент для обработки больших массивов информации.